Coverlutional Neural Networks (CNNs)

常见的卷积结构

基本卷积

No padding, no strides	Arbitrary padding, no strides	Half padding, no strides	Full padding, no strides
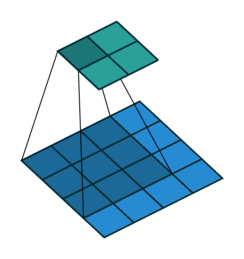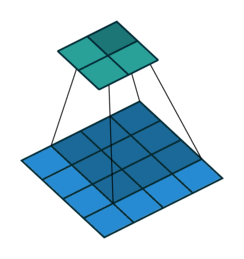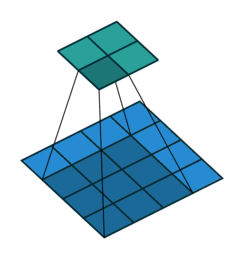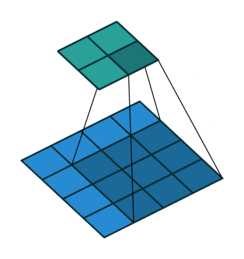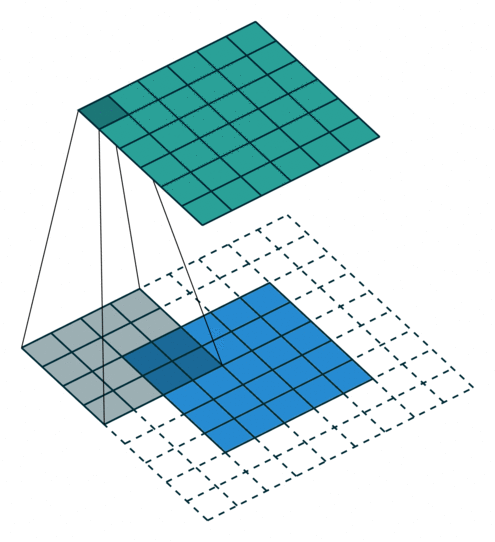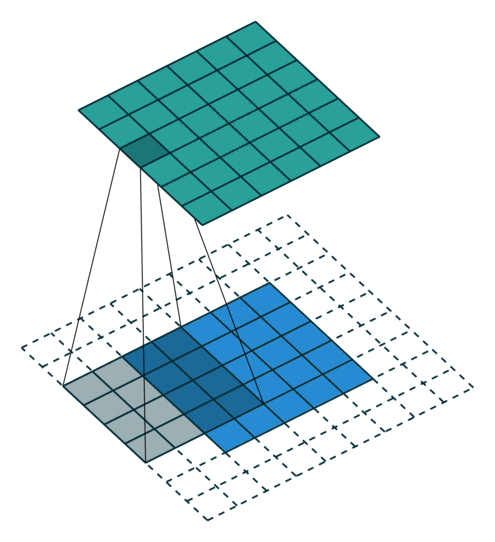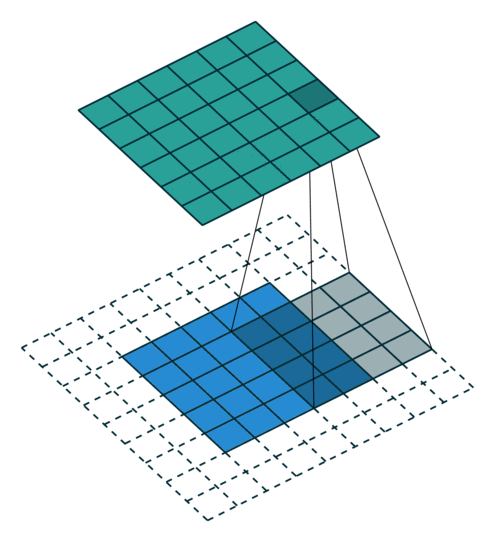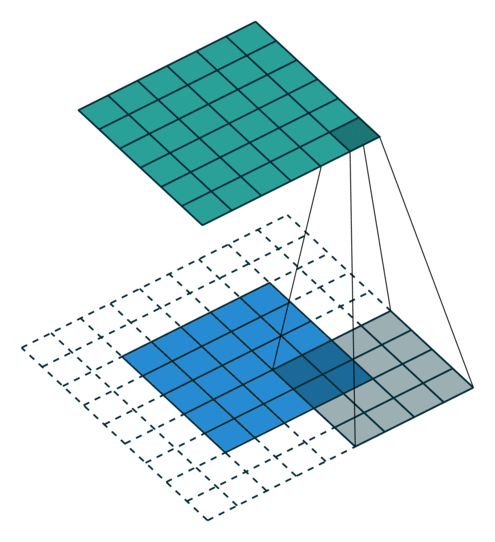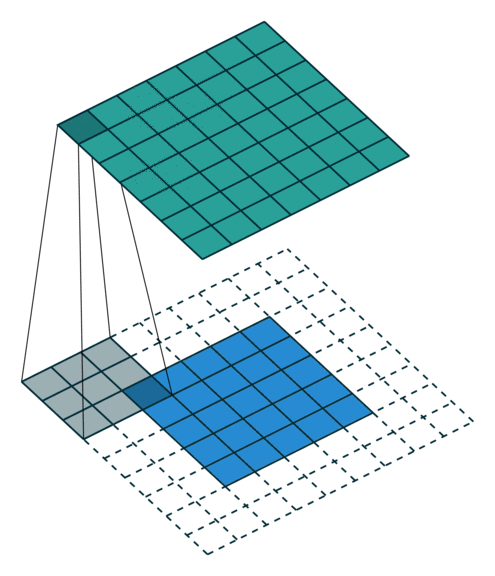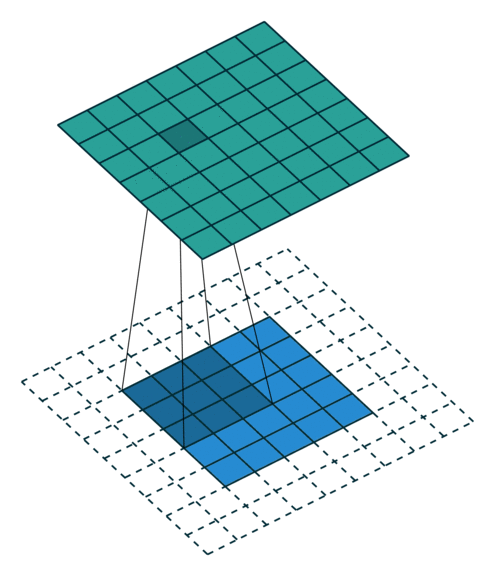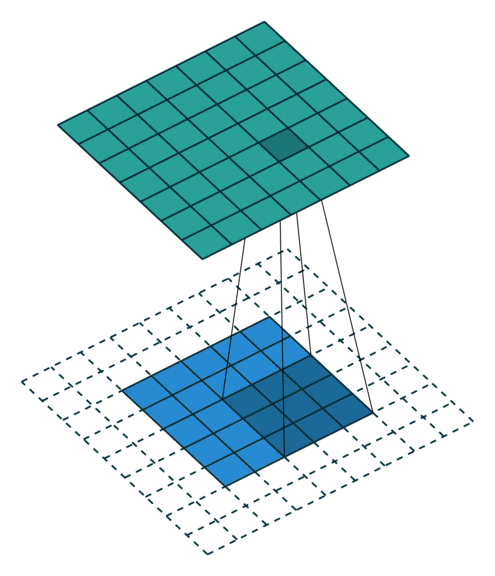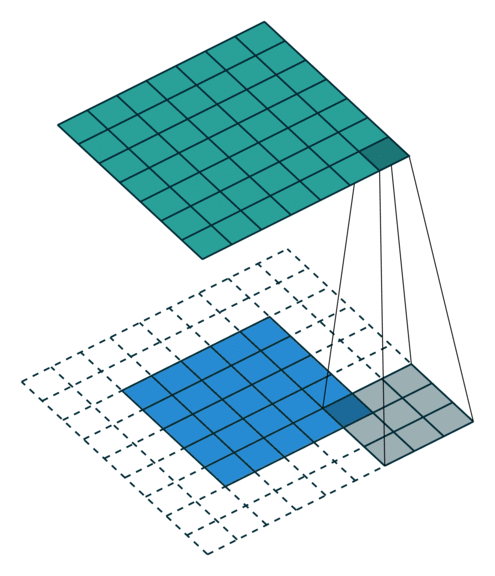No padding, strides	Padding, strides	Padding, strides (odd)

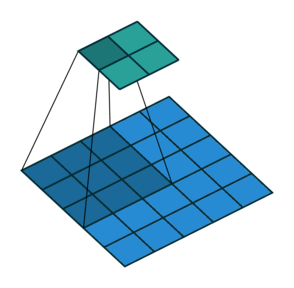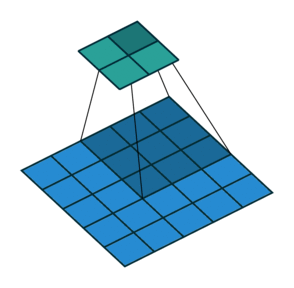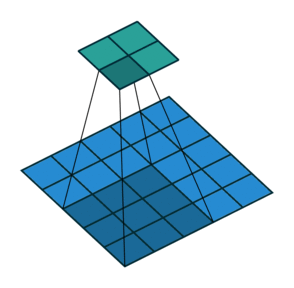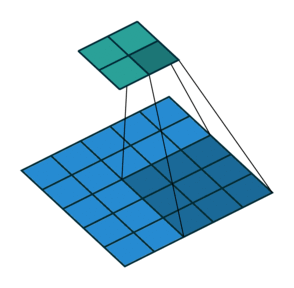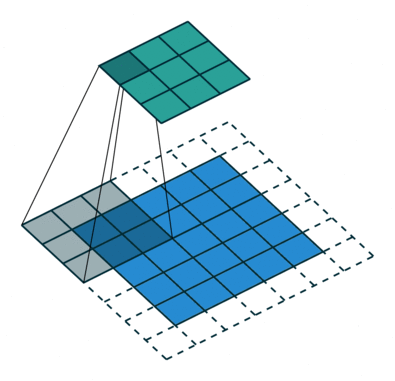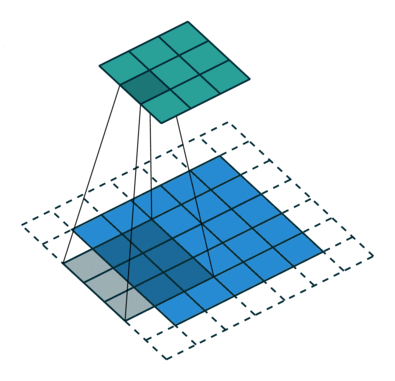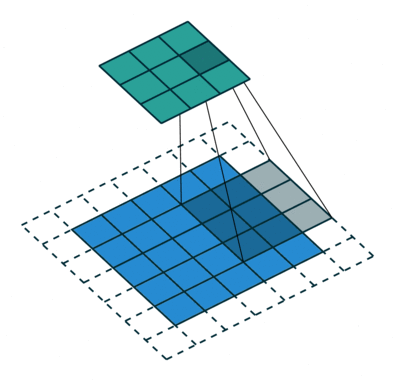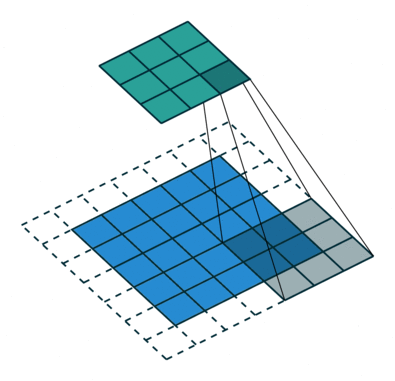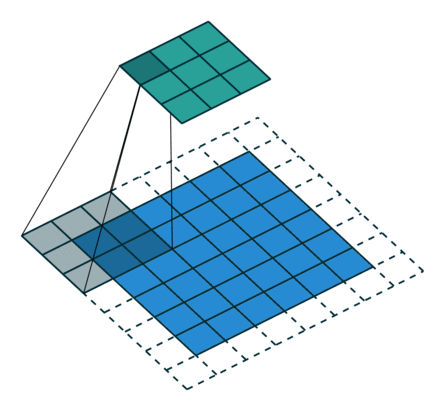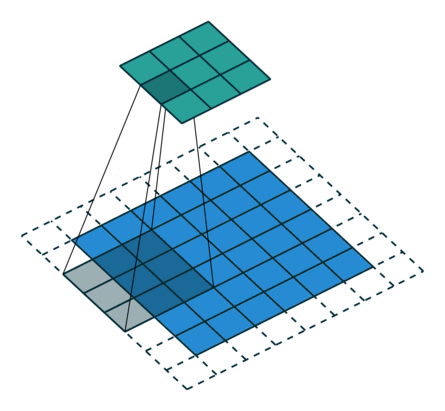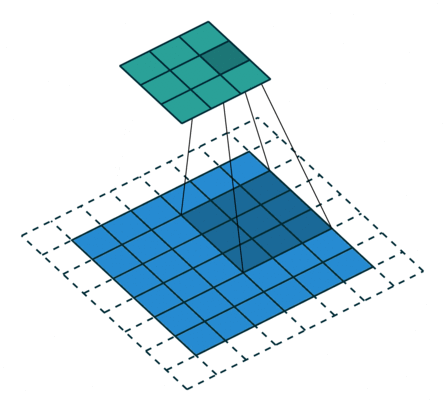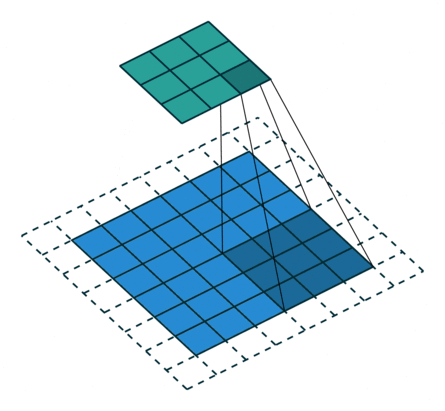转置卷积

• 转置卷积（Transposed Convolution），又称反卷积（Deconvolution）、Fractionally Strided Convolution
• 转置卷积是卷积的逆过程，如果把基本的卷积（+池化）看做“缩小分辨率”的过程，那么转置卷积就是“扩充分辨率”的过程。
• 为了实现扩充的目的，需要对输入以某种方式进行填充。
• 转置卷积与数学上定义的反卷积不同——在数值上，它不能实现卷积操作的逆过程。其内部实际上执行的是常规的卷积操作。
• 转置卷积只是为了重建先前的空间分辨率，执行了卷积操作。
• 虽然转置卷积并不能还原数值，但是用于编码器-解码器结构中，效果仍然很好。——这样，转置卷积可以同时实现图像的粗粒化和卷积操作，而不是通过两个单独过程来完成。

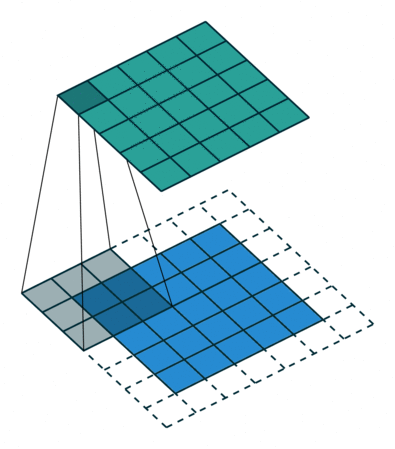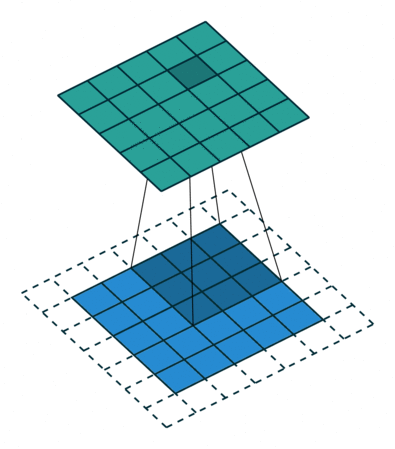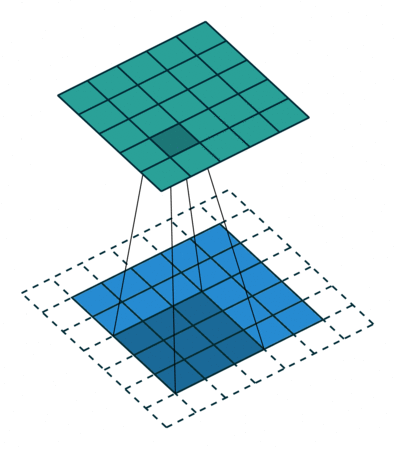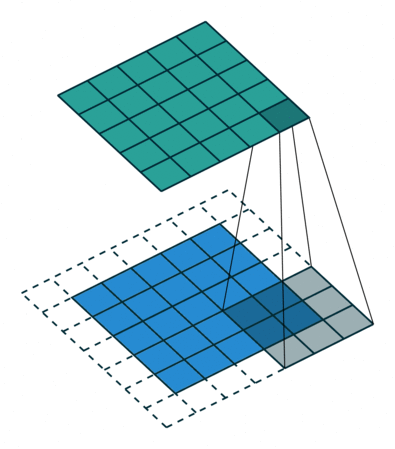
No padding, no strides, transposed	Arbitrary padding, no strides, transposed	Half padding, no strides, transposed	Full padding, no strides, transposed
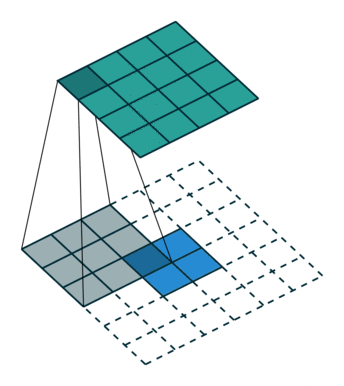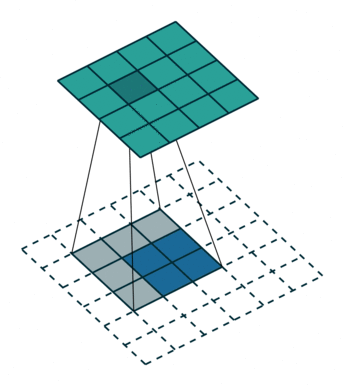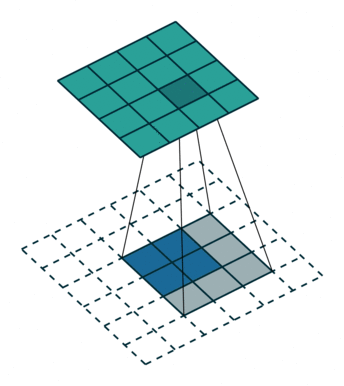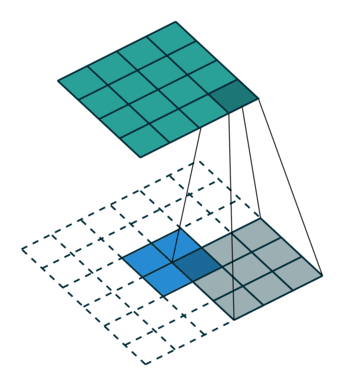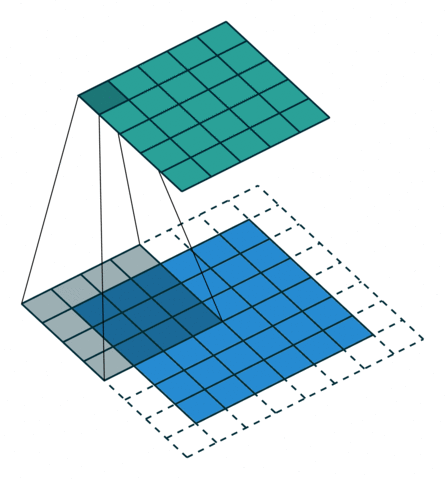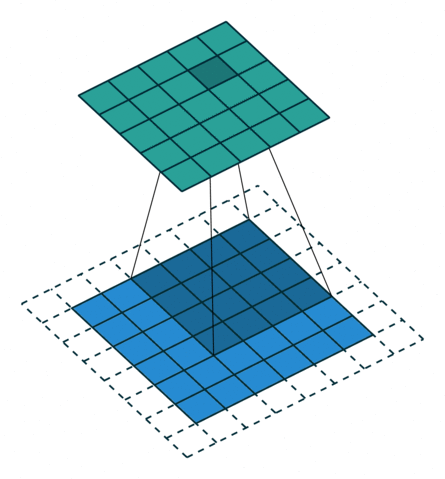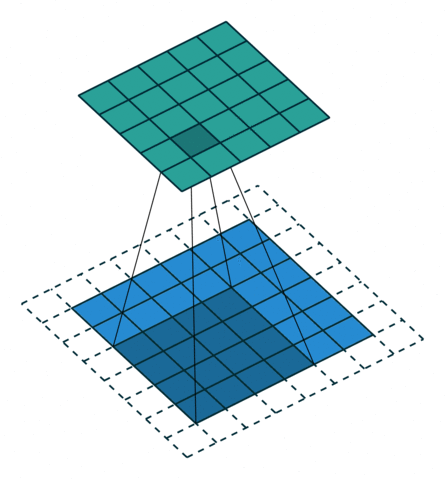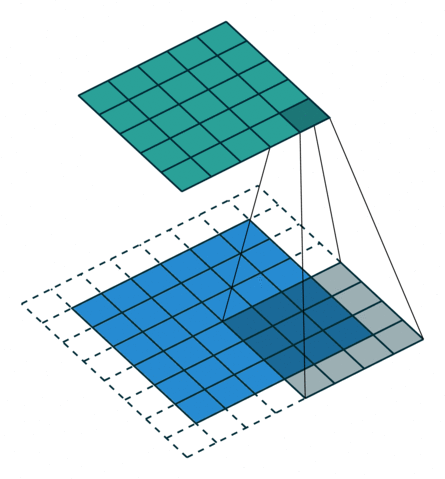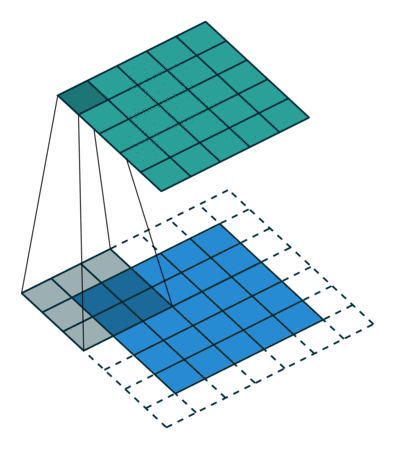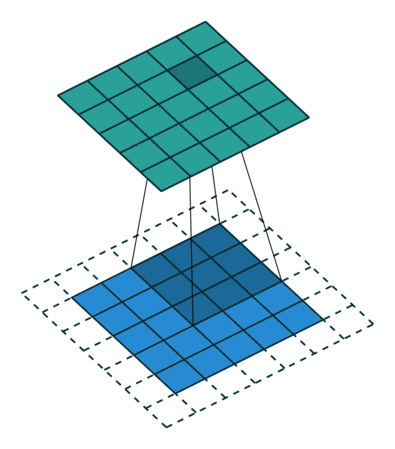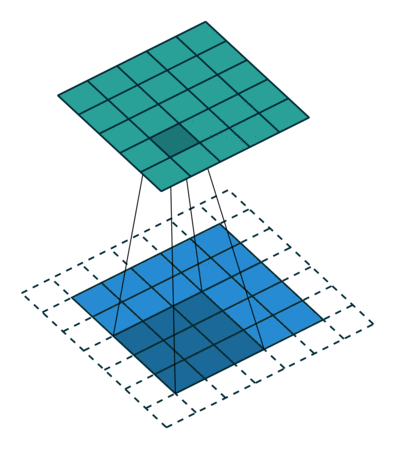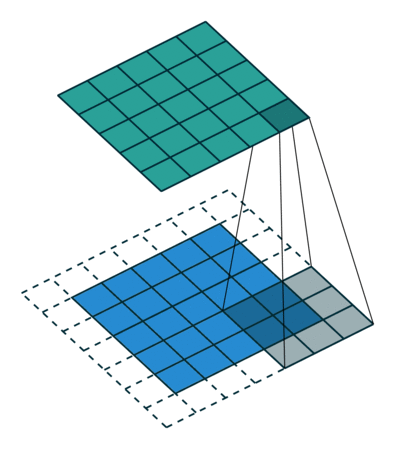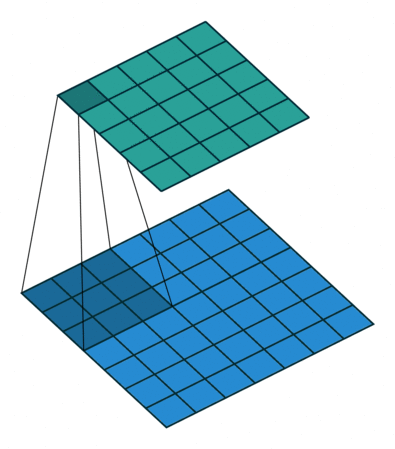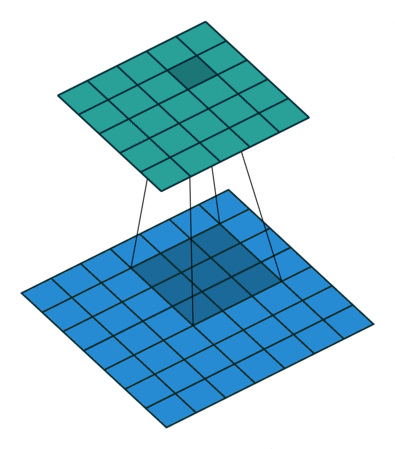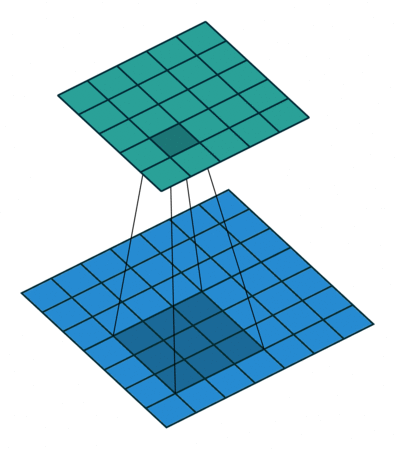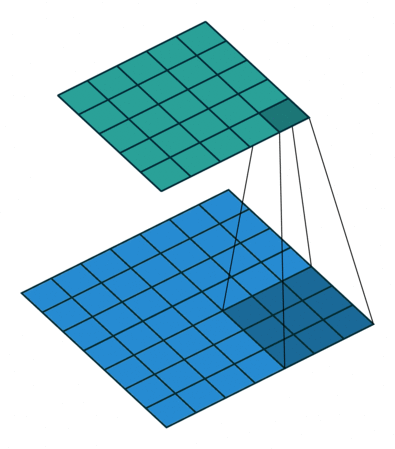No padding, strides, transposed	Padding, strides, transposed	Padding, strides, transposed (odd)

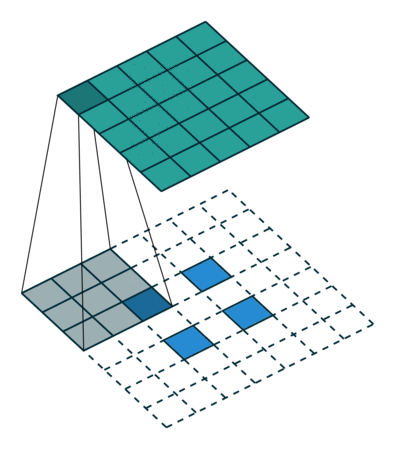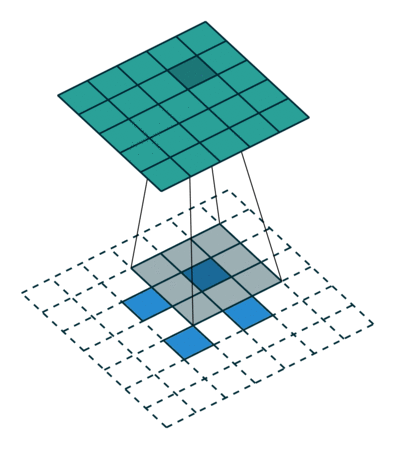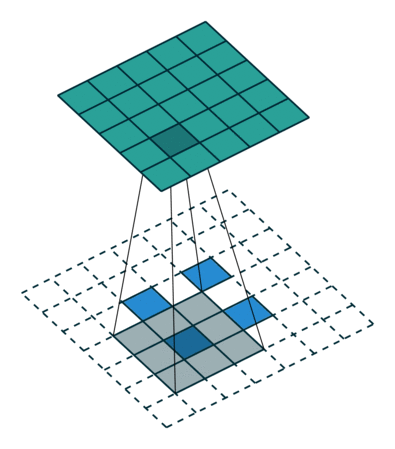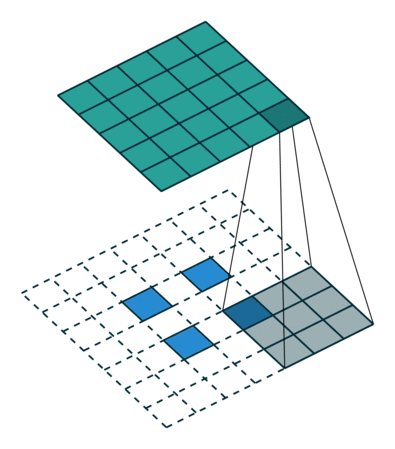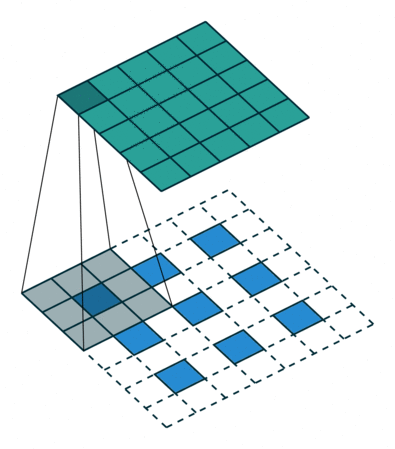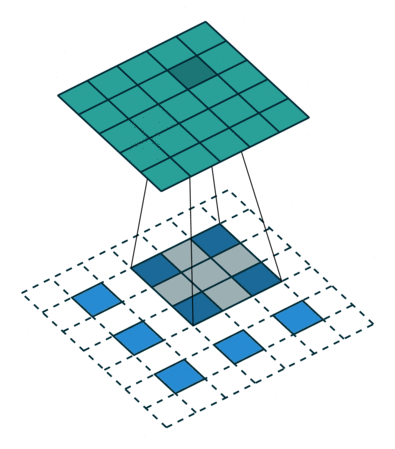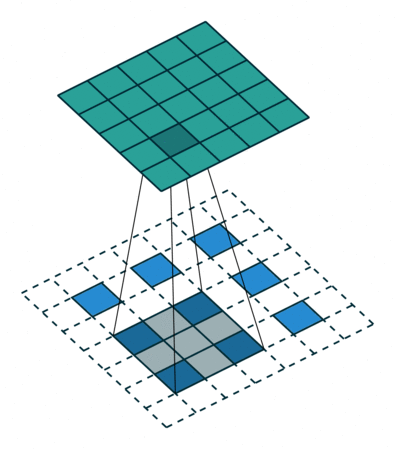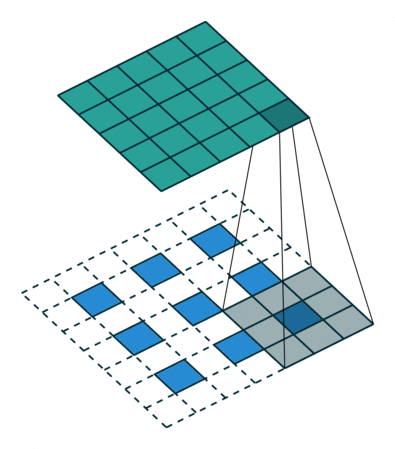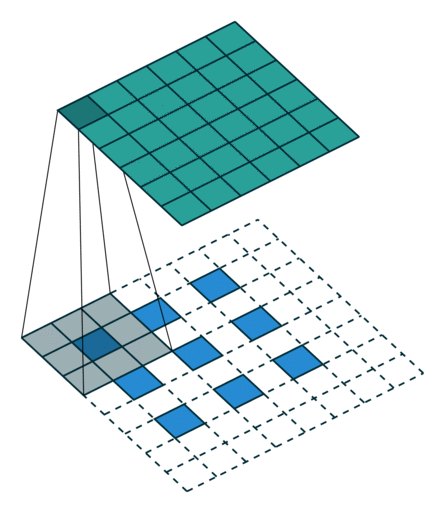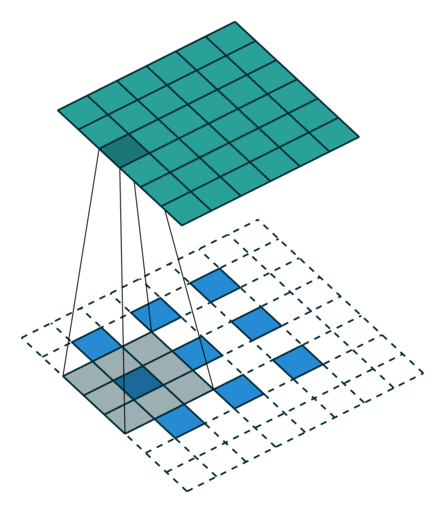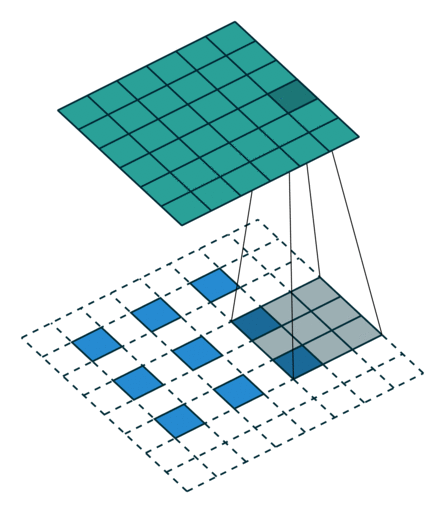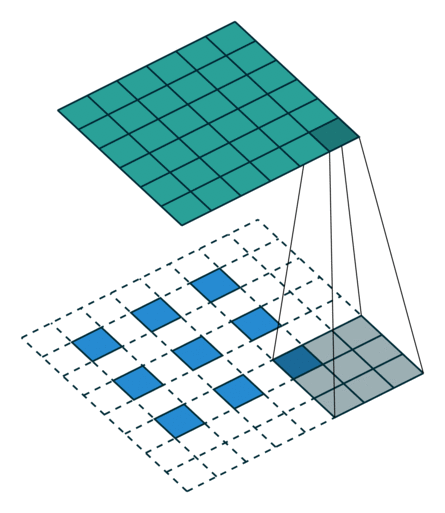空洞卷积

• 空洞卷积（Atrous Convolutions）也称扩张卷积（Dilated Convolutions）、膨胀卷积。

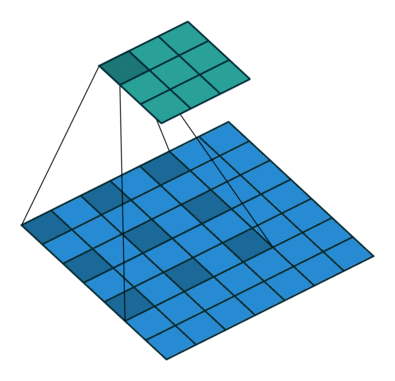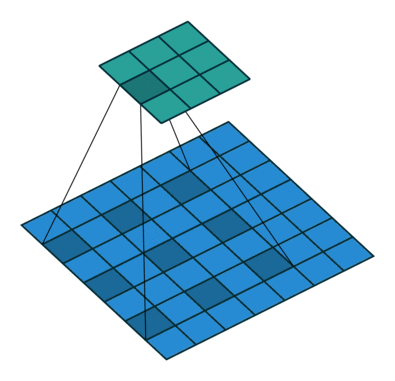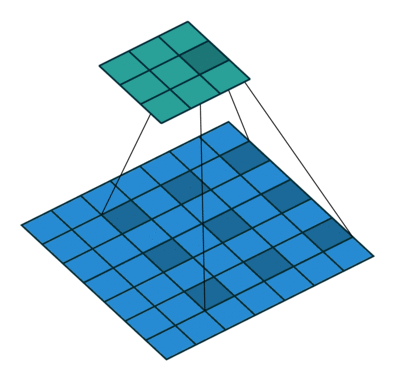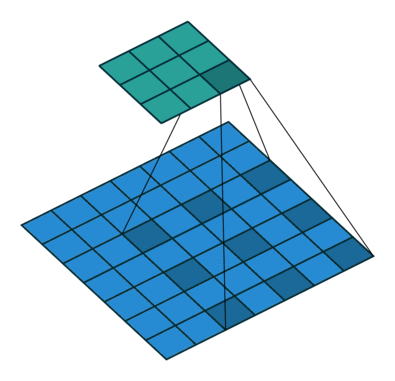
No padding, no strides.

空洞卷积的作用

• 空洞卷积使 CNN 能够捕捉更远的信息，获得更大的感受野；
• 同时不增加参数的数量，也不影响训练的速度。

示例：Conv1D + 空洞卷积

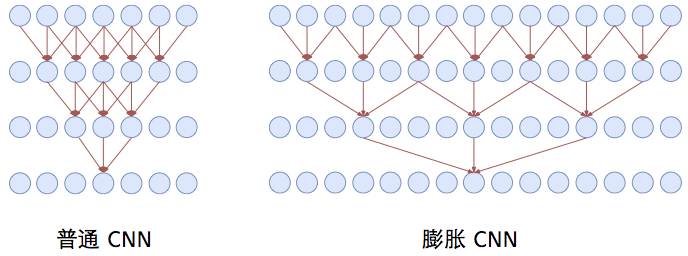
可分离卷积

• 逐通道卷积

Depthwise Convolution的一个卷积核负责一个通道，一个通道只被一个卷积核卷积。

一张5×5像素、三通道彩色输入图片（shape为5×5×3），Depthwise Convolution首先经过第一次卷积运算，DW完全是在二维平面内进行。卷积核的数量与上一层的通道数相同（通道和卷积核一一对应）。所以一个三通道的图像经过运算后生成了3个Feature map(如果有same padding则尺寸与输入层相同为5×5)，如下图所示。

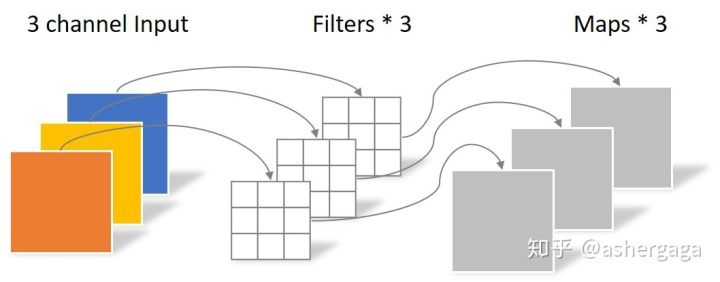
Depthwise Convolution完成后的Feature map数量与输入层的通道数相同，无法扩展Feature map。而且这种运算对输入层的每个通道独立进行卷积运算，没有有效的利用不同通道在相同空间位置上的feature信息。因此需要Pointwise Convolution来将这些Feature map进行组合生成新的Feature map。

• 逐点卷积

Pointwise Convolution的运算与常规卷积运算非常相似，它的卷积核的尺寸为 1×1×M，M为上一层的通道数。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个卷积核就有几个输出Feature map。

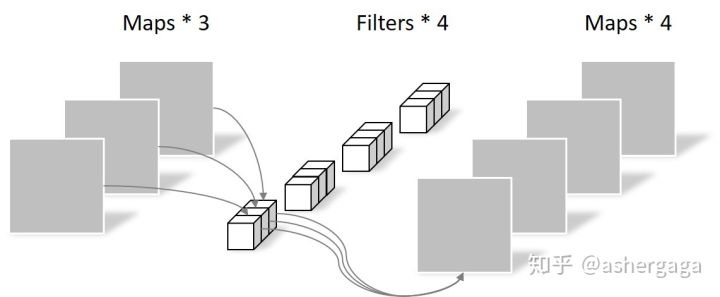
经过Pointwise Convolution之后，同样输出了4张Feature map，与常规卷积的输出维度相同。

门卷积

• 类似 LSTM 的过滤机制，实际上是卷积网络与门控线性单元（Gated Linear Unit）的组合。

• 核心公式

  

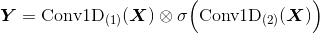
  中间的运算符表示逐位相乘—— Tensorflow 中由 tf.multiply(a, b) 实现，其中 a 和 b 的 shape 要相同；后一个卷积使用sigmoid激活函数。

• 一个门卷积 Block

  

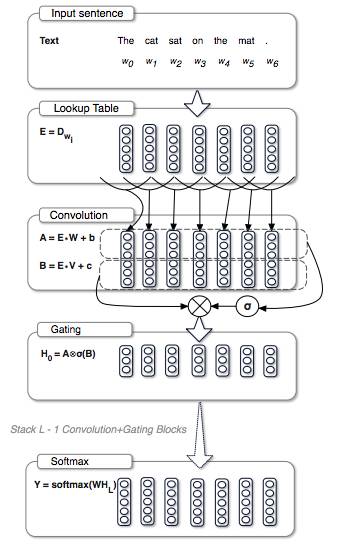
  W 和 V 表明参数不共享。

• 实践中，为了防止梯度消失，还会在每个 Block 中加入残差

门卷积的作用

• 减缓梯度消失
• 解决语言顺序依存问题

门卷积是如何防止梯度消失的

• 因为公式中有一个卷积没有经过激活函数，所以对这部分求导是个常数，所以梯度消失的概率很小。

• 如果还是担心梯度消失，还可以加入残差——要求输入输出的 shape 一致。

  

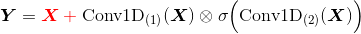
  更直观的理解：

  

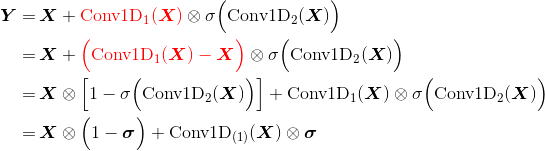
  即信息以 1-σ 的概率直接通过，以 σ 的概率经过变换后通过——类似 GRU

  因为Conv1D(X)没有经过激活函数，所以实际上它只是一个线性变化；因此与 Conv1D(X) - X 是等价的

CNNs与DNNs

CNNs相对于DNNs的优点

• CNNs的特征就是共享卷积核，对高维数据处理无压力。图像通过卷积操作后仍然保留原先的位置关系。

• DNNs的输入是向量形式，并未考虑到平面的结构信息，在图像和NLP领域这一结构信息尤为重要，例如识别图像中的数字，同一数字与所在位置无关（换句话说任一位置的权重都应相同），CNNs的输入可以是tensor，例如二维矩阵，通过filter获得局部特征，较好的保留了平面结构信息。

CNNs结构总结

• 卷积层：对图像元素的矩阵变换，是提取图像特征的方法，多种卷积核可以提取多种特征。一个卷积核覆盖的原始图像的范围叫做感受野（权值共享）。一次卷积运算(哪怕是多个卷积核)提取的特征往往是局部的，难以提取出比较全局的特征，因此需要在一层卷积基础上继续做卷积计算 ，这也就是多层卷积。
• 池化层：降维的方法，按照卷积计算得出的特征向量维度大的惊人，不但会带来非常大的计算量，而且容易出现过拟合，解决过拟合的办法就是让模型尽量“泛化”，也就是再“模糊”一点，那么一种方法就是把图像中局部区域的特征做一个平滑压缩处理，这源于局部图像一些特征的相似性(即局部相关性原理)。
• 全连接层：softmax分类
• 训练过程：卷积核中的因子(×1或×0)其实就是需要学习的参数，也就是卷积核矩阵元素的值就是参数值。一个特征如果有M个值，N个特征就有M*N个值，再加上多个层，需要学习的参数还是比较多的。
• CNNs filter尺寸计算：Feature Map的尺寸等于(input_size + 2 * padding_size − filter_size)/stride + 1

The link of this page is https://blog.nooa.tech/articles/7203e497/ . Welcome to reproduce it!