Activation Functions

背景

在不使用激活函数的情况下，神经网络的每一层节点的输入都是上层输出的线性函数。很容易验证，无论神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron），此时的神经网络拟合能力相当有限。正因为这个原因，我们需要引入非线性函数作为激活函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。

激活函数的主要形式

在此从形式以及存在的问题方面介绍几种常用的激活函数，Sigmoid，tanh，ReLU（包括LeakyReLU，pReLU，ELU），Maxout，Softmax以及Softplus。

Sigmoid

形式

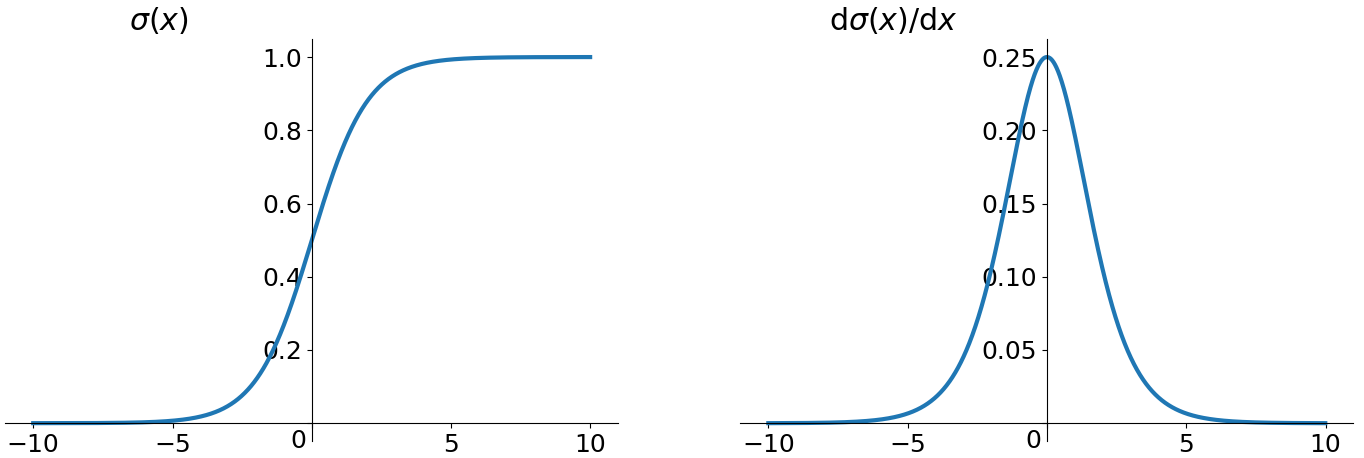
我们从Sigmoid（S形曲线）激活函数说起，刚开始认识Sigmoid可能是从Logistic Regression开始，它的形式如下：

$$f(z)=\frac{1}{1+e^{-z}}$$

对应的坐标系表示为：

问题

1. 有饱和区域，是软饱和，在大的正数和负数作为输入的时候，梯度就会变成零，使得神经元基本不能更新。
2. 只有正数输出（不是zero-centered），这就导致所谓的zigzag现象。
3. 计算量较大

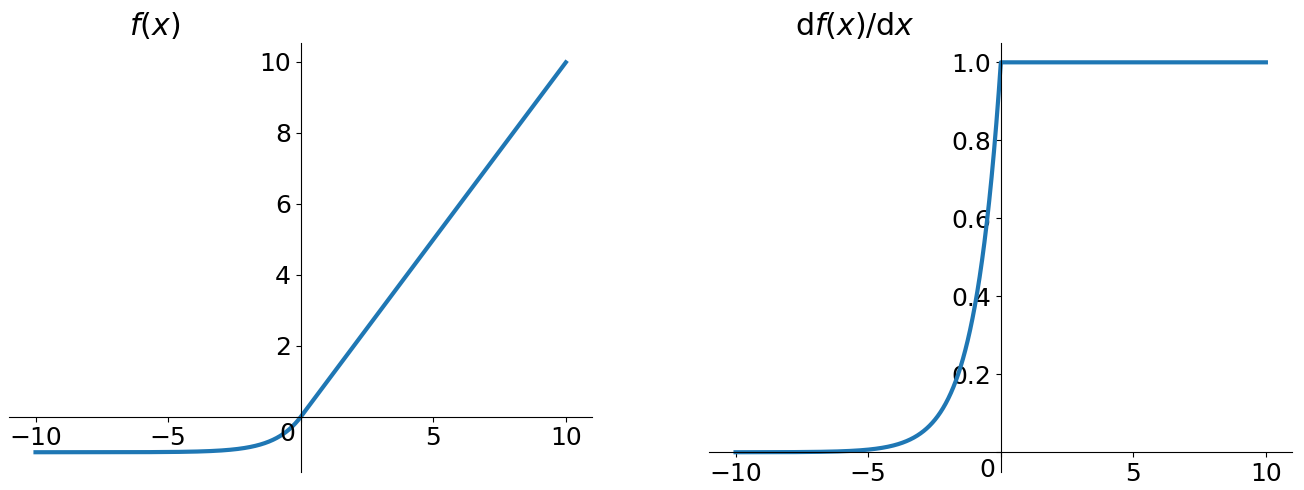
tanh

形式

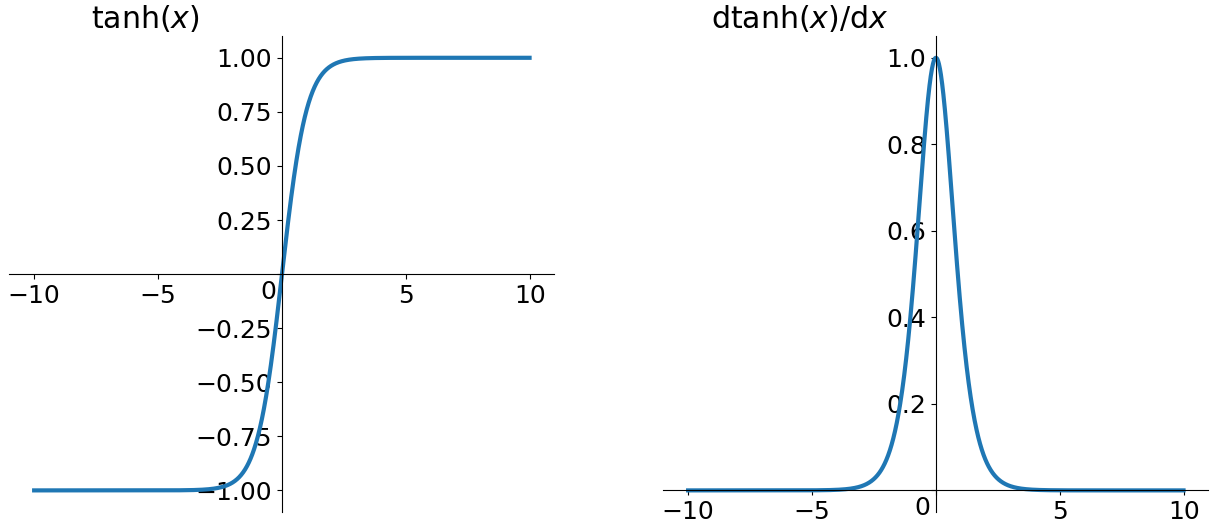
其作为改进版的Sigmoid，数学形式及对应的曲线如下：

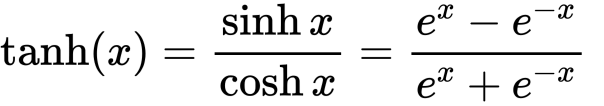
问题

1. tanh是zero-centered，但是还是会饱和，这就导致在输入值较大或者较小时，倒数趋近于0。

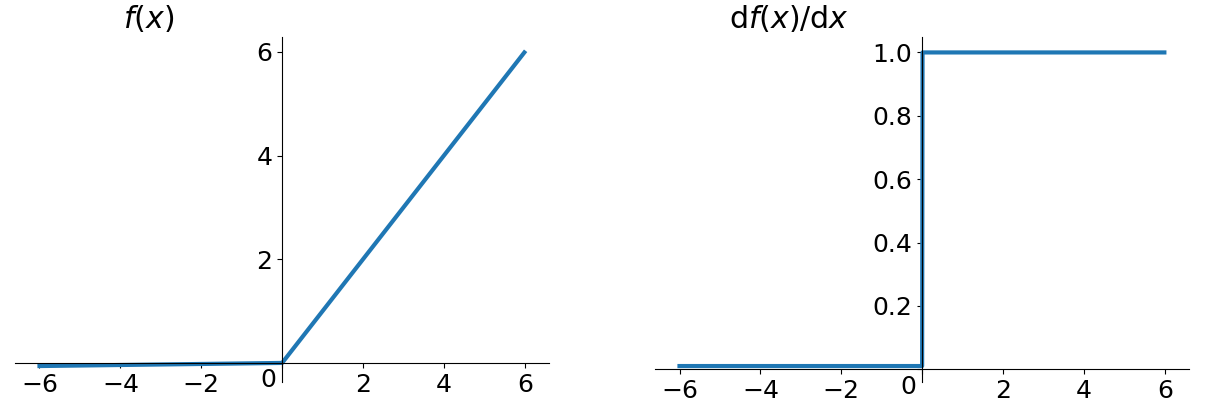
ReLU（Rectified Linear Unit）

形式

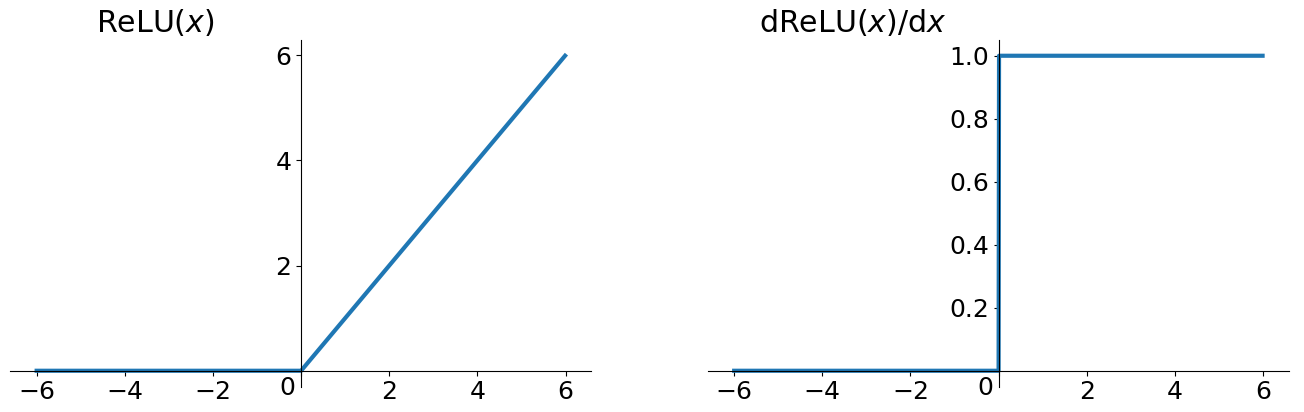
ReLU的形式比较简单，省去了exp的计算，因而计算量小，收敛较快。当输入大于0的时候返回原输入值，当输入小于0的时候返回0，即f(x) = max(0, x)。

问题

1. 非zero-centered。
2. 在负数区域被killed的现象叫做Dying ReLU。

针对ReLU的改进

为了解决Dying ReLU问题，有三种比较常用的解决方案。

LeakyReLU

LeakyReLU的思想是直接将x ≤ 0的部分修改为较小的0.01x，于是整体的形式就变成了f(x) = max(0.01x, x)。

pReLU (Parametric ReLU)

其形式为f(x) = max(ax, x)，其中a通过学习得到，而不是固定的。

ELU（Exponential Linear Unit）

其形式表示为：f(x) = max(α(exp(x) - 1), x)。

Maxout

Maxout是通过分段线性函数来拟合所有可能的凸函数来作为激活函数的，但是由于线性函数是可学习，所以实际上是可以学出来的激活函数。具体操作是对所有线性取最大，也就是把若干直线的交点作为分段的界，然后每一段取最大。

其形式为：

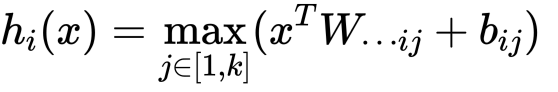
Softmax

也称归一化指数函数，其一般形式为：

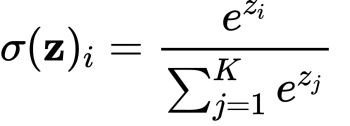
Sigmoid函数如果用来分类的话，只能进行二分类，而Softmax函数可以看做是Sigmoid函数的一般化，可以进行多分类。

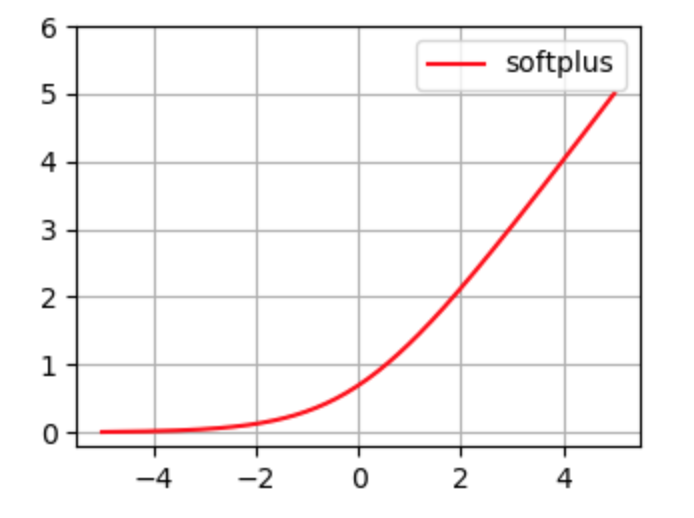
Softplus

其一般形式为：

$$f(x) = \ln \left(1+e^{x}\right)$$

The link of this page is https://blog.nooa.tech/articles/7af9d25d/ . Welcome to reproduce it!