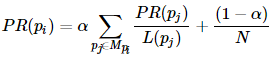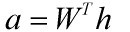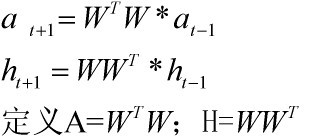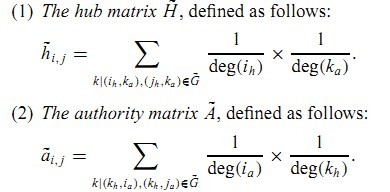PageRank算法预先给每个网页一个PR值（PR值指代PageRank值），PR值在物理意义上为一个网页被访问的概率，所以一般是1/N，其中N为网页总数。
另外，所有网页的PR值的和一般为1。（如果实在不为1也不是不行，最后算出来的不同网页之间PR值的大小关系仍然是正确的，只是这个数值不能直接地反映概率罢了。）
接着，运用下面的算法不断迭代计算，直至达到平稳分布为止。
普通情况
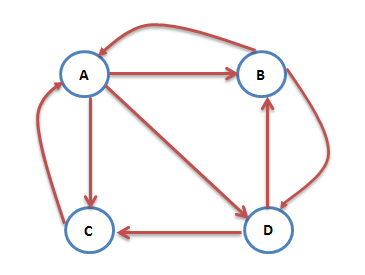
互联网中的众多网页可以看成一个有向图，箭头的指向即为链接的链入，根据上图，我们得到A的PR值为：PR(A)=PR(B)/2+PR©/1。
没有出链
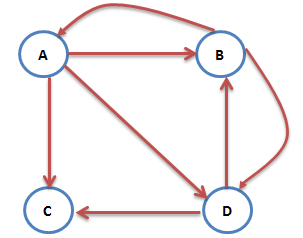
网络中不乏一些没有出链的网页，如上图，其中，网页C没有出链，也就是说网页C对其他网页没有PR值的贡献，我们不喜欢这种“自私”的网页（其实是为了满足 Markov 链的收敛性），于是设定其对所有网页（包括它自己）都有出链，则此图中A的PR值表示为：PR(A)=PR(B)/2+PR©/4。
出链循环圈
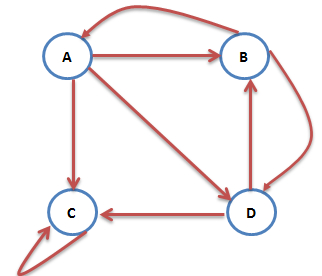
网络中还存在这样的网页：只对自己有出链，或者几个网页的出链形成一个循环圈。那么在不断迭代的过程中，这一个或几个网页的PR值将只增不减，这显然是不合理的。
那么如何解决这个问题呢？我们假设某人正在浏览网页C，显然他不会一直停留在网页C，他可能会随机地输入一个网址从而去往另一个网页，并且其跳转到每个网页的概率是一样的。于是此图中A的PR值表示为：PR(A)=∂(PR(B)/2)+(1-∂)/4。
综上，一般情况下，一个网页的PR值计算公式如下：
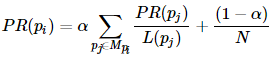
其中，Mpi是所有对pi网页有出链的网页集合，L(pj)是网页pj的出链数目，N是网页总数，α一般取0.85。
根据上面的公式，我们就可以计算出每个网页的PR值，在不断迭代并趋于平稳的时候，即为最终结果。
HITS算法
算法简介：
首先把那些根据关键相关返回网页作为根集合S，再由S集合网页节点的链入和链出网页节点派生出结合C，结合C包括S，链入和链出节点集合。
C中的每个节点分配一对权重<h(s),a(s)>, 节点h(s)权重由节点链出的节点的a(s)决定，a(s)由节点的链入节点的h(s)决定。
算法过程：
网页的a权重向量：
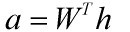
关于HITS算法收敛性，可以从如下变换形式来得出：
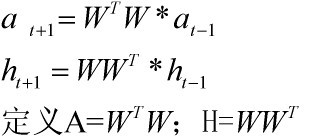
当算法收敛时候，a其实就是对应矩阵A那个最大特征值对应的特征向量的归一化形式，同样，h也是H矩阵那个最大特征值对应的特征向量的归一化形式。
算法实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
class HITSIterator:
__doc__ = '''计算一张图中的hub,authority值'''
def __init__(self, dg):
self.max_iterations = 100
self.min_delta = 0.0001
self.graph = dg
self.hub = {}
self.authority = {}
for node in self.graph.nodes():
self.hub[node] = 1
self.authority[node] = 1
def hits(self):
"""
计算每个页面的hub,authority值
:return:
"""
if not self.graph:
return
flag = False
for i in range(self.max_iterations):
change = 0.0
norm = 0
tmp = {}
tmp = self.authority.copy()
for node in self.graph.nodes():
self.authority[node] = 0
for incident_page in self.graph.incidents(node):
self.authority[node] += self.hub[incident_page]
norm += pow(self.authority[node], 2)
norm = sqrt(norm)
for node in self.graph.nodes():
self.authority[node] /= norm
change += abs(tmp[node] - self.authority[node])
norm = 0
tmp = self.hub.copy()
for node in self.graph.nodes():
self.hub[node] = 0
for neighbor_page in self.graph.neighbors(node):
self.hub[node] += self.authority[neighbor_page]
norm += pow(self.hub[node], 2)
norm = sqrt(norm)
for node in self.graph.nodes():
self.hub[node] /= norm
change += abs(tmp[node] - self.hub[node])
print("This is NO.%s iteration" % (i + 1))
print("authority", self.authority)
print("hub", self.hub)
if change < self.min_delta:
flag = True
break
if flag:
print("finished in %s iterations!" % (i + 1))
else:
print("finished out of 100 iterations!")
print("The best authority page: ", max(self.authority.items(), key=lambda x: x[1]))
print("The best hub page: ", max(self.hub.items(), key=lambda x: x[1]))
if __name__ == '__main__':
dg = digraph()
dg.add_nodes(["A", "B", "C", "D", "E"])
dg.add_edge(("A", "C"))
dg.add_edge(("A", "D"))
dg.add_edge(("B", "D"))
dg.add_edge(("C", "E"))
dg.add_edge(("D", "E"))
dg.add_edge(("B", "E"))
dg.add_edge(("E", "A"))
hits = HITSIterator(dg)
hits.hits()
|
SALSA算法
SALSA算法和HITS算法初始部分一样，构建相同的集合集C和彼此的链接关系。
SALSA一种随机游走过程，但是不同经典的随机游走。它涉及到把一个网页节点看成2种不同类型节点：hub和authority，随机游走对应着这样两种不用类型的Markov链：hub链和authority链，状态转移为网页前向和后向。
首先是把构建一个无向图，原图节点分为2类，然后构建边。
这样从某个节点出发，进行两个方向的随机游走。h和a方向的状态转移矩阵：
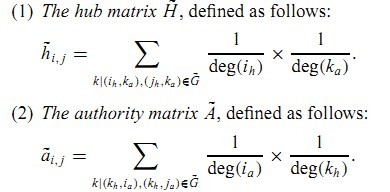
对于以上的形式可以通过如下的矩阵相乘的方式展现：
有了H和A矩阵，就可以知道节点集合最终的h和a向量：和HITS一样，h和a对应H和A的最大特征值对应的归一化特征向量。其实，计算h和a可以参照HITS，进行迭代求解。
The link of this page is https://blog.nooa.tech/articles/82a6b55c/ . Welcome to reproduce it!
