微积分(Calculus)

2018-02-04 Mathematical Modeling

微积分（Calculus）

微积分的主要内容

求导公式
乘积法则
链式法则
隐函数求导
积分、微分的互逆关系
泰勒级数

微积分的三个中心思想：

积分
微分
积分与微分的互逆

积分的直观理解 - 推导圆的面积

回顾圆的面积公式：

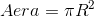
如何从积分的角度推导出圆的面积公式？

不同的划分方法会带来不同的积分公式，下面考虑将圆划分为大量的同心圆环，这种方法保留了圆的对称性。

考虑其中一个环的面积，可以将其看做一个“类矩形”

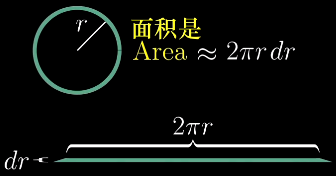
虽然这不是标准的矩形，但只要dr越小，它就越接近。它的面积可表示为：

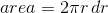
于是，圆的面积可以看作是这一系列矩形面积的叠加。

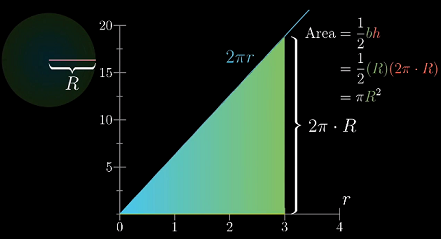
这部分面积的求和可以等价于求“函数y = 2πr图像在区间[0, R]下的面积”。

这个推导的过程其实可以看作是对函数y = 2πr在[0, R]下的积分。

积分与导数

直观来说，对函数f(x)在[a, b]上积分就是求函数f(x)在区间[a,b]下的图像与坐标轴包围的面积。记作：

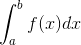
这实际上是定积分的概念，此外还有不定积分。

如果是其他图像，比如抛物线，该怎么求这部分的面积呢？

能不能找到一个函数 A(x) 表示 0 到 x 之间函数图像下的面积？——这个函数 A(x) 就是该函数的积分（函数）。

这里强调 0 到 x 之间，是为了使问题具有实际意义

以抛物线 f(x)=x^2 为例。类似的，我们可以将这块区域划分成一系列细长的矩形。

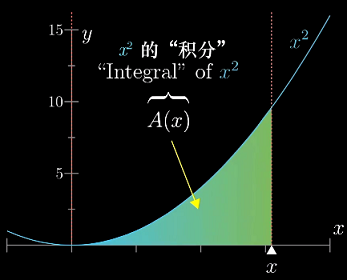
将 x 增加 dx，增加的面积可以看做是一个长f(x)、宽dx的矩形，只要dx越小，这条窄带就越接近矩形。

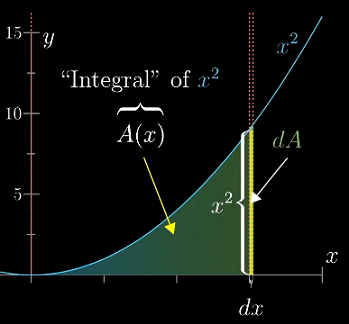
把这部分面积记作 dA，表示面积的微小变化（difference in Area）

通过这个矩形，可以得到 A、f(x) 与 dx 之间的关系：

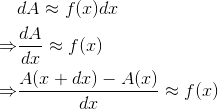
这里引出了微积分中另一个重要的概念——导数。dA/dx 就是 “A 的导数”

更严格的说法是："A 的导数"是“当 dx → 0 时，dA/dx 所趋向的值”。（下一节会讨论导数的定义）

一般不会刻意区分导数和导数函数的区别，都统称为导数，具体含义视语境而定；同样，积分也是如此。

导数是解决积分问题的关键——积分需要还原出某个导数原本的函数——如果你能熟练的计算导数，那么你也能解决这个问题。

积分与导数之间的这种互相转化的关系，也就是“某个图像下方面积函数的导数能够还原出定义这个图像的函数”，就叫做微积分基本定理。该定理表明，“在某种意义上”，两者互为逆运算。

导数（Derivative）

“瞬时变化率”引起的歧义 — 导数的悖论

“瞬时变化率”的歧义——只有在不同的时间点之间，变化才能发生；而将时间限制在某个瞬间点的时候，变化也就不存在了。

考虑这个示例：一辆车从 A 点起，先加速，再减速，至 100 米外的 B 点停下，整个过程花费 10 秒。

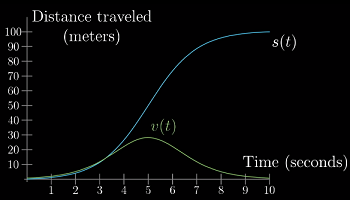
把车速的图像加入其中，可以发现：两者存在着某种联系：其中之一改变的话，也会引起另一个发生变化。

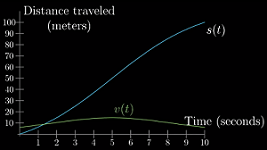
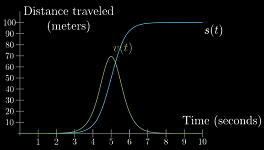
直觉上，速度越大，距离-时间函数的图像也越陡峭，意味着车在单位时间内移动的距离更长

速度的大小是如何随着距离-时间函数的变化而变化的？——“瞬时”速度的矛盾：

在绘制速度图像的时候，需要给每个单独的时间点关联一个速度值，但是计算速度却需要两个时间点上的距离。
记时间差为 dt，距离差为 ds，那么这段时间内的速度就能用 ds/dt 表示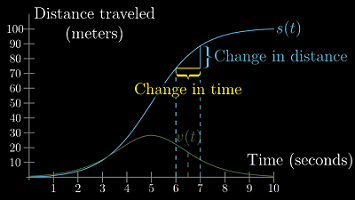

当年的微积分创始人们也经历了同样的思维冲突。
换言之，速度只有在一段会时间内的才有意义；“瞬时”的说法会带来矛盾
实际的做法是：会选取一个很小的 dt 值，然后把 ds/dt 看做是这个瞬间的速度。

导数的定义与计算

导数的定义

在纯数学领域，导数不是 dt 为某个具体值时 ds/dt 的值，而是当 dt 的值无限逼近 0 时这个比值的极限。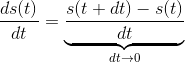
从图像的角度，（某一点的）导数有一个直观的含义：就是经过图像上该点切线的斜率。
注意：这里的 dt 不是“无穷小”，也不是 0；它永远是一个有限小的量，接近 0 而不是 0。

这种说法在试图规避“瞬时”带来的矛盾，使“某个时间点的变化率”有意义。

导数的计算

抛开求导公式，先来看一下面对一个实际的问题，该如何求解（在某一点处的）导数。
对于 s(t)=t^3 在 t=2 处的导数，根据导数的定义，有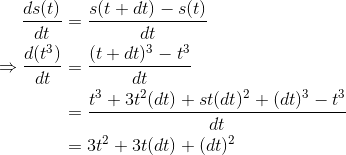
当 dt 趋向 0 时，后两项也会趋于 0，进而消去。代入 t=2 可以得到在该点处的导数为 12
更一般的，称 s'(t) = 3*t^2 为 s(t) = t^3 的导函数。

对于常见的函数，有一系列总结出的求导公式可以快速计算（下一节会演示如何从几何的角度来推导这些公式）

导数的含义是“变化率的最佳近似”

回顾之前关于距离-速度的示例，思考这个问题：当 t=0 时，车在不在移动？
一方面，利用导函数公式可以得到 t=0 时的速度为 0——这似乎在说“车没有移动”；另一方面，如果车在 0 时刻没有移动，那么它是何时开始移动的？——关键在于这个问题本身就是没有意义的。
因为导数并不是用来测量“瞬时变化”的。
t=0点的导数为 0 的真正含义是指“在第 0 秒附近，车速的最佳近似为 0 米/秒”——换句话说，就是当时间间隔 dt 越来越小时，表示速度的比值 ds/dt 就越趋向于 0——这并不表示车在 0 时刻就是静止的，只能说它此时的速度近似于 0.

用几何来求导

为什么导数很重要？——当需要使用微积分来解决现实中的实际问题时，需要将其抽象成各种代表性的函数来描述；而如果能掌握这些抽象函数的变化率，那你就学会了这门可以精准描述事物变化率的语言。

从几何的角度看“微小变化量”

以 f(x) = x^2 为例：

从坐标轴上看，x^2 的图像是一条抛物线，我们已经知道，导数可以描述为切线的斜率
此外，x^2 还有另一个更直接的含义：长为 x 的正方形的面积。
假如给边长 x 一个微小的增量 dx，那么正方形的增量（变化量）是多少？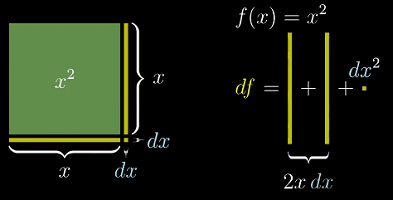
应该时刻记住的 dx 是一个微小的量——这意味着你可以忽略所有次数高于 1 的 dx 项——换言之，一个微小量的平方（或更高次方）是一个可以忽略的变化量
由此，可以得到：
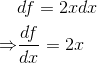
上一节给出了 f(x) = x^3 导数的代数推导过程，这里也可以作为立方体体积来用几何的方式推导。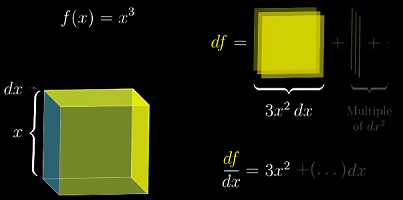

负的变化量

上述两个例子的变化量都是增量（正值），但实际上变化量也可能是负值，比如 f(x) = 1/x——考虑这样一个特殊的矩形，长 x，宽 1/x，它的面积恒为 1.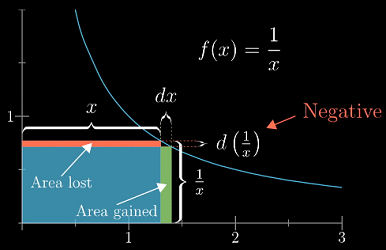

注意：这里的变化量不再是矩形的面积了，而是矩形的高
通过简单的几何知识，可知矩形高的变化量为：
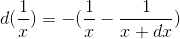
从而得到 1/x 的导数为：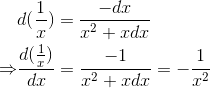

幂函数的导数

以上 x^2、x^3 和 x^-1 都遵循了幂函数的求导公式：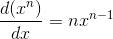
思考一下为什么这个公式也适用于 2 和 3 以外的指数——求导的一个关键点在于很大一部分项因为包含 dx 的高次幂，可以被忽略——因此有
当指数小于 0 时，会更复杂一些——比如 x^-2 可以考虑一个边长为 √x 的正方形。

大多数时候，我们都有合适的求导公式来使用，但是以上利用几何求导的过程能锻炼我们借助微小变化量来考虑的导数的能力。

三角函数的导数

正弦函数的定义
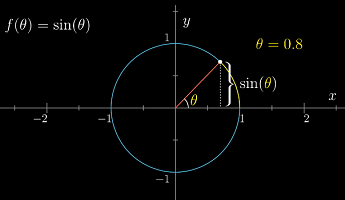
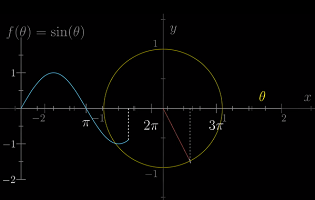
- θ=0.8 表示单位圆弧长为 0.8 时对应的角度为 θ（单位圆的周长为 2π）
- sin(θ) 表示此时该点距离 x 轴的高度（可能为负）
- 当 θ 增加时，sin(θ) 的值会在 -1 到 1 之间上下摆动
sin(θ) 当 θ 增加时的微小变化量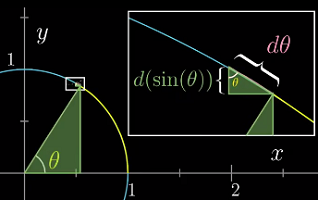
- 在近似的观点下，应该有这样的直觉——可以把那一段微小的圆弧dθ看作是直线
根据三角函数的定义，有

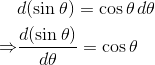
直观理解链式法则

求导公式概览：

函数的和/差——加法法则
函数的积/商——乘法法则
复合函数的求导法则

加法法则

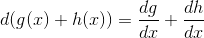
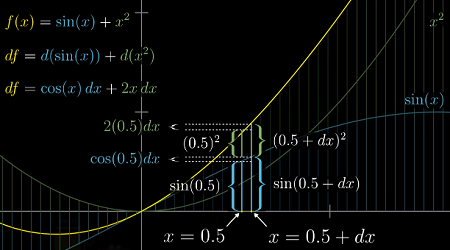
加法法则比较简单，可以在坐标轴中展示

乘法法则

“左乘右导 + 右乘左导”：

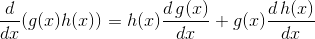
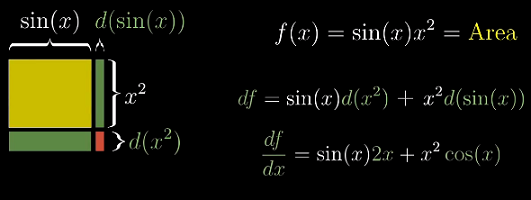
在数学中，如果你要处理两项的乘积，用面积来理解会更方便

复合函数的求导法则 — 链式法则

链式法则：

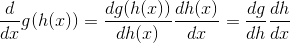
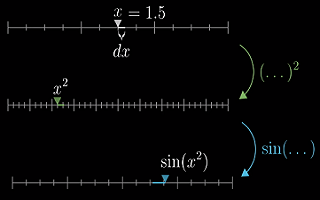
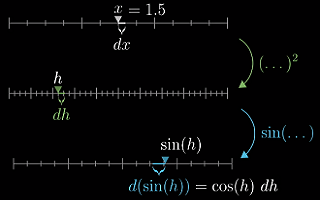
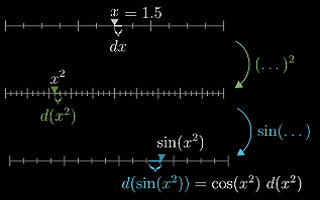
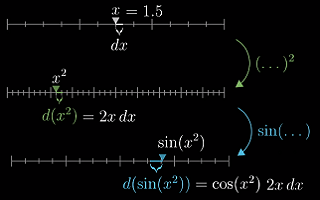
链式法则的表达式在说：看看输出值 g 的微小变化除以 h 的微小变化是多少（h 是要带入函数 g 中的值）；然后乘以 h 微小变化与 x 微小变化的比值

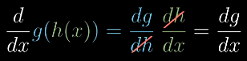
这些 dh 最终会被消去，结果就是输出值 g 的微小变化与输入值 x 的微小变化的比值

dh 的消去并不只是符号上的技巧，而是真实反映出在求导时，各微小变化量发生了什么。

指数函数的导数 — 自然常数 e 的定义

从2^t开始：

根据导数的定义，有
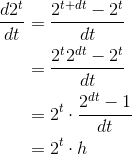
当 dt → 0 时，h 趋向于一个常数 0.6931...
也就是说，2^t 图像上各点处切线的斜率 = 该点的函数值 * 一个常数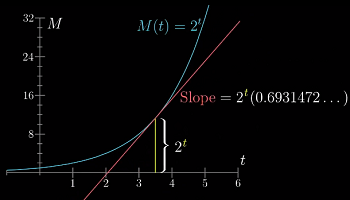
类似的，3^t 也存在这样一个 h=1.0986...；8^t 则是 h=2.0794...
注意到，8^t 的 h 大概是 2^t 的三倍，而 8^t = 2^{3t}

是否存在某个数，使 h 恰为 1？——这个数就是自然常数 e

e^t 时，h=1的原因是因为e就是如此定义的。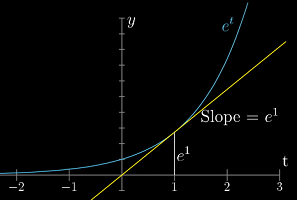

和“为什么π正好等于圆的周长比直径”一样，π就是这么定义的。

自然常数不是完全这样发现的，但过程类似

指数函数的导数

有了自然常数 e 以及链式法则，就可以求出其他指数函数的导数了
根据指数函数的性质与链式法则，有
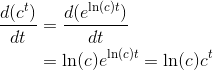
事实上，在微积分中，指数函数基本都是以 e^ct 的形式出现的，很少会直接使用 c^t 的形式

为什么称 e 为自然常数？

现实世界中，很多自然现象里的变化率与变化量是成正比的
比如：在室温环境下，热水变凉的速率与水和房间的温差成正比（或者说，温差的变化率与温差本身成正比）
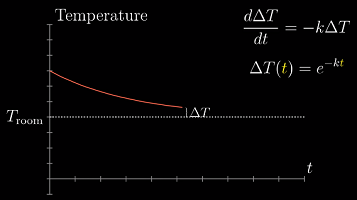
尽管指数函数有多种写法，但是将其表达为以 e 为底的幂函数是非常自然的。
因为 e 有着非常自然的含义，它就是变化率与数量本身的比例系数。

隐函数求导

什么是隐函数？

如果方程 F(x,y)=0 能确定 y 是 x 的函数，那么称这种方式表示的函数是隐函数；
直观来说，就是满足某种关于变量 x 和 y 的关系的、所有 (x, y) 点的集合，相应的曲线就是“隐函数曲线”。

示例 1：圆上某一点切线的斜率

圆的方程就是一个隐函数，比如 x^2 + y^2 = 5^2，下面需要求圆上一点的斜率（不考虑几何方法）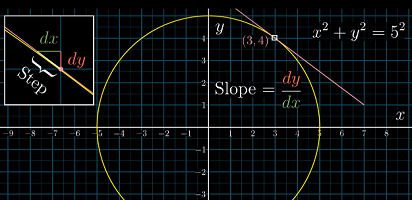
因为这里的曲线并不是一个函数图像，所以不能单纯对其求导——它不存在变量 x 的微小变化对函数值 y 的微小变化
当然，如果我们的目标只是求 dy/dx，那么对等式两边同时求导可以解决：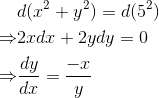

示例 2：相关变化率

这是一个更实际的例子：开始时，梯子上端距地面 4m(y=4)，下端距墙 3m(x=3)。如果梯子的上端以 1 m/s 的速度下滑，那么下端左滑的速度是多少？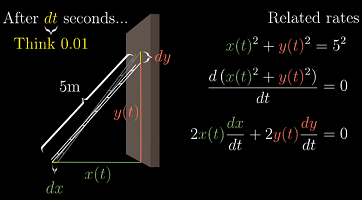
等式的左边可以看做是一个关于时间 t 的函数，于是对表达式左边求导的含义相当于在问“经过短暂的时间 dt，y 会减少一点，x 会增加一点，那么整体的变化量是多少？”，而表达式右边告诉我们这个变化量为 0。
带入 x(t)=3, y(t)=4, dy/dt=1，就能求出 dx/dt 了。

隐函数求导的含义

从纯数学的角度看，示例 1 与示例 2 的做法没有区别。但是示例 2 求导时带有明确的物理意义——表达式随时间的变化率。但是求圆切线时似乎难以解释为什么这么做。
其实隐函数的导数也是一个隐函数，它对 dx 和 dy 的关系做了限制——在圆的例子上，它要求整体变化量 dS = 2xdx + 2ydy 为 0；也就是说为了让 S = x^2 + y^2 始终保持在 25，那么 dS 就需要为 0.

严格来讲，这个条件实际上是保证每一步落在过该点的切线上，而不是落在圆本身。当 dx 和 dy 足够小时，这两者才没有区别。

在隐函数的导数中，原来的变量看做常数，比如这里 2xdx + 2ydy = 0 中的 x 和 y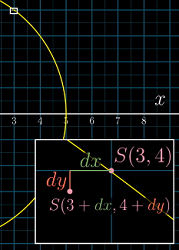

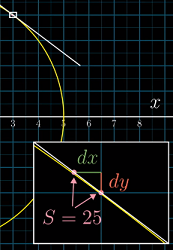
显然，（左）的正体变化量就不满足使 S 保持不变

示例 3：sin(x)y^2 = x

该函数的图像是一系列 U 型曲线

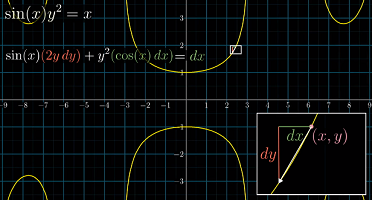
有了这个等式，就能方便求出 dy/dx 了。
对表达式的两边求导，就可以得到导数的隐函数，它对 x 和 y 的整体微小变化量作出了限制。

示例 4：ln(x)的导数——从已有的导函数推算出其他函数的导函数

根据指数函数与对数函数的关系，有

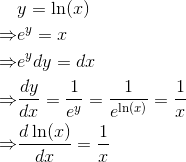
多元微积分

隐函数求导是多元微积分的入门。两者的要点是一样的，需要理解这多个变量是如何联系在一起变化的。

极限

简单来说，“极限”就是逼近/趋近更“洋气”的说法。

导数的正式定义

导数的计算公式：

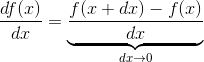
导数的正式定义：

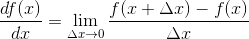
或

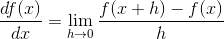
为什么不用 dx？——dx 本身已经表达了求极限的含义——使用 dx 的表示容易将其理解成“无穷小的变化量”；更正确的解读应该是把它看做一个具体的、有限小的变化量，并时刻考虑 dx → 0 时的情况。

为什么用一个新的变量 h？——明确变化量 h 只是一个普通的数，跟“无穷小”没有任何关系。

极限的 `(ϵ, δ)` 定义

所谓极限，指的是变量逼近 0 时的影响，而非无穷小变量的影响

导数由极限定义，而极限本身由 (ϵ, δ) 定义，下面是比较书面的说法：

设函数f(x)在点x0的某一去心邻域内有定义，如果存在常数a，对于任意给定的正数ϵ，都∃δ>0，使不等式|f(x)-a| < ϵ在|x-x0| ∈ (0,δ)恒成立，那么a就叫做函数f(x)当x→x0时的极限，记作

极限存在与不存在的两个例子

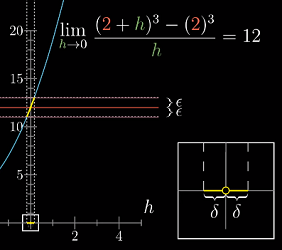
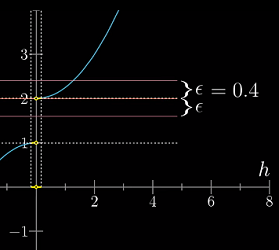
极限存在的前提是，你总能在距离极限点x0距离为δ(>0)的取值范围内，找到一系列取值点，使得范围内的任一取值点，它的函数值都在距离f(x0)为ϵ(>0)的范围内——关键在于这种情况对于任意ϵ都成立——无论ϵ多小，你总能找到与之对应的δ

利用导数来求极限——洛必达法则

如果函数在点x0处是有定义的，那么该点的极限值 == 函数值本身。

如果函数在该点没有定义呢？比如 sin(πx)/(x^2-1)，该函数在x0=±1处就没有定义。

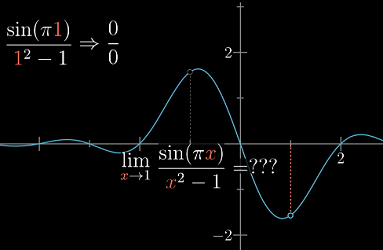
洛必达法则

洛必达法则专门用于求解 0/0 型和 ∞/∞ 的极限值。
导数是由极限定义的，但反过来，也能利用导数来求极限
洛必达法则利用了这样一个性质——当f(a)=0时，在a的附近，有f(a+dx)=f'(a+dx)。如图所示：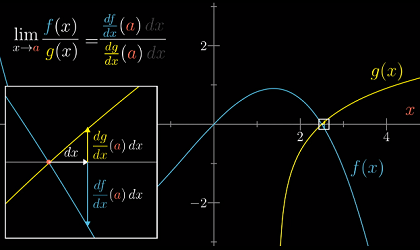

当 dx 越小，这个比值就越精确
洛必达法则：

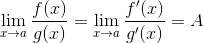
条件：1）f(x)和g(x)在点a处的极限都为 0；2）f(x)和g(x)在点a的某去心领域内可导，且g'(x)!=0；3）A可以为实数，也可以为±∞

注意，只要满足以上条件，洛必达法则是可以继续进行的
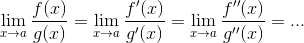
这么看，实际上，求解导数的过程也是在使用洛必达法则

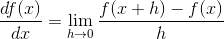
分子分母在 h→0 处的极限都为 0

积分与微积分基本定理

积分其实就是求导的逆运算

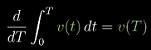
示例：距离是速度对时间的积分

已知速度-时间的关系 v(t)=t(8-t)，求这段时间驶过的距离。
现在“已知每个时间点的速度 v(t)，来求距离s(t)”
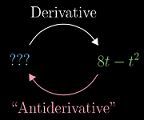
从数学的角度，前者的问题等价于求“s(t)的导数”，于是现在的问题也就是求“哪个函数的导数是v(t)”——这通常被称为“求函数的‘原函数’（或‘反导数’）”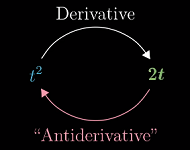
这个问题可以转化成求解曲线下方的面积
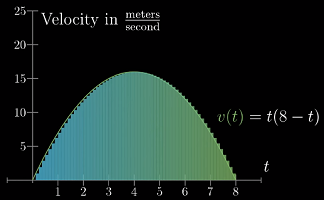
这个过程可以表示为 v(t) 的“积分”：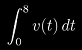

为什么不适用∑？——∫指的并不是具体的dt的加和，而是当dt→0时，加和逼近的值，这个逼近的值就是曲线下方的面积；当dt越趋近 0，加和就越趋近精确解。

积分的含义就是将所有小量“累积”在一起
“求函数图像与横轴围成的面积”是许多不相干问题的共通之处——可以被拆成小量，然后近似为这些小量的和

积分与导数是一组互逆的运算

根据以上的分析，距离实际上是速度对时间的积分，而速度是距离对时间的导数——这表明积分与导数是一组互逆的运算

面积函数的导数等于函数本身

如果固定左端点，将右端点当做一个变量 T，那么这个积分可以看做以上限为自变量的函数 s(T)——这是距离关于时间的导数，同时也是图形下方的面积函数
这表明任一函数图像下方面积函数的导函数等于该函数本身
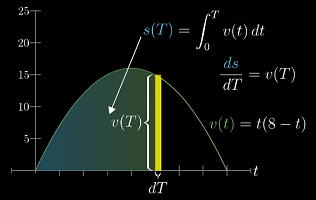
- 从几何的角度看，矩形的面积为 ds，宽为 dT，它的高为 v(T)，于是有 ds/dT = v(T)
- 即图像所表示的函数就是面积函数的导数
因此，求解积分的过程就是求导的逆过程

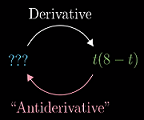
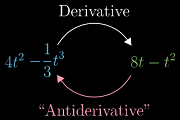
每个函数都有无数个原函数

因为常数的导数为 0，所以在原函数的基础上加上任意常数，其导数不变——这意味着每个函数的原函数有无数个
所以v(t) = 8t - t^2正确的原函数应该是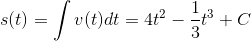
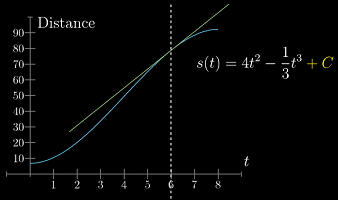
从图像上来看，曲线上下移动并不会影响其在每一点的斜率
在不同的问题中，一般会有额外的条件帮你决定该使用哪个原函数
- 比如，在本问题中，t=0 时，s(t)=0，于是 C=0

8.2. 微积分基本定理

在对任意函数求（定）积分时，你是在对 x 在一定范围内的所有 f(x)*dx 求和，而积分值就是 dx → 0 时，这个和趋近的值。
求积分的第一步是找出原函数 F，使其导数为积分内的函数。
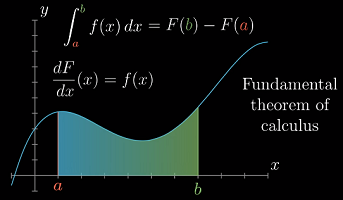
积分值就等于原函数在上限时的值减去其在下限时的值。
这个过程就是“微积分基本定理”
积分异于常识的一点在于：它连续地遍历了从下限到上限中的每一个自变量的值，而我们在利用原函数求值时，只需要关注上限与下限两个自变量

负面积

如果图像有部分出现在横轴的下方，那么这部分就是负面积

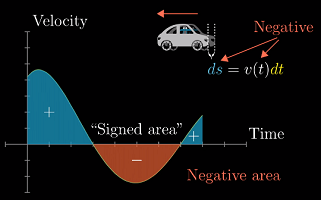
有符号的面积
积分计算的不是真正的面积，而是图像与横轴围城的带有正负的面积。

连续变量的平均值

结论：区间上的平均斜率等于起点和终点连线的斜率

如何求连续变量的平均值？

问题等价于求图像下方面积的平均高度
如果把面积作为一个整体来看，这是一个很简单的问题——平均高度 = 积分面积 / 上下限宽度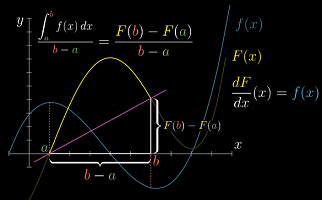
值得注意的是，(F(b)-F(a))/(b-a) 实际上也是原函数F(x)在 x=a 和 x=b 两点连线的斜率
这表明在某一区间上所有点处切线的平均斜率等于起点和终点连线的斜率

根据定义，f(x)是其原函数F(x)的导函数，也就是说它给出了F(x)在每个点上切线的斜率，所以f(x)在(a,b)上的平均值也就是原函数从x=a到x=b上所有切线斜率的平均值。
换言之，求解连续函数的平均值，可以转化为求解其原函数在各点切线的平均斜率；而两点间的平均斜率等于这两点的斜率。

适用“积分”的场景

可以通过细分然后相加的方式进行估算时
求解连续变量的均值时（特别在概率中）

泰勒级数

高阶导数

这里介绍高阶导数的目的是帮助得到函数的近似——泰勒级数

二阶导数描述的是曲线的弯曲程度

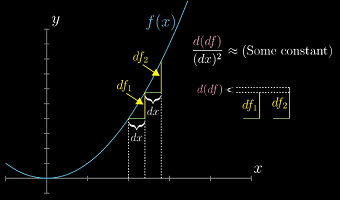
根据导数的定义，二阶导数也就是导数的微小变化率，即斜率的变化率——直观来看，也就是曲线的弯曲程度
- 考虑函数的一个取值 x，然后向右连续的增加两个小量 dx
- 第一个增量是函数产生了第一个变化量 df1，第二个同理，记 df2
- 这两个变化量的差也就是函数值变化量的变化量，记 d(df). 它和 (dx)^2 成正比
- 所谓二阶导数，就是 d(df) 和 (dx)^2 当 dx → 0 时比值的极限
用符号表示为

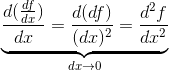
其实中间的写法才是最正确的，但为了书写方便，通常写成最右侧的形式
一个理解二阶导数的现实示例就是加速度

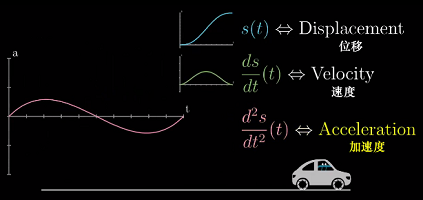
二阶导数为正，说明车在加速；反之，为负，说明在减速

泰勒多项式与泰勒级数

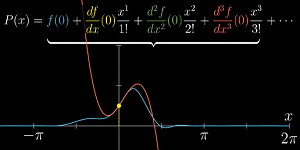
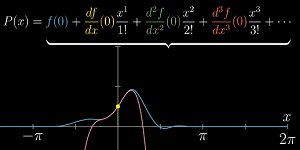
泰勒级数的作用——函数近似工具。比如，在 x=0 附近，有：

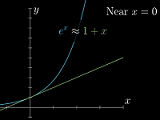
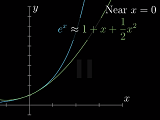
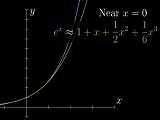
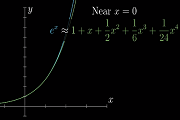
泰勒级数利用多项式函数去近似复杂抽象的函数，从而化简问题

多项式函数的优势：易计算、易求导、易积分
深度学习中的梯度下降（一阶）、牛顿法（二阶）也是利用的泰勒级数

示例：cos(x) 在 x=0 附近如何用二次多项式近似？

问题等价于在所有可能的 c0 + c1*x + c2*x^2 中确定系数使其在 x=0 附近最近似 cos(x)
不考虑任何先验知识，看看只凭直觉应该怎么确定这三个系数
- 首先，cos(x) 在 x=0 处等于 1，那么至少多项式这一点要满足，即 c0=1
- 如果多项式在 x=0 处切线的斜率也与 cos(x) 相同，那么近似程度应该会更高，于是 c1=0
- 二阶导数描述的是曲线的弯曲程度，那么让两个图像在 x=0 处的弯曲程度相同应该会更近似，cos(x) 的二阶导是 -cos(x)，于是 2c2=-cos(0)=-1 -> c2=-1/2
- 还可以用更高次的多项式去近似，比如
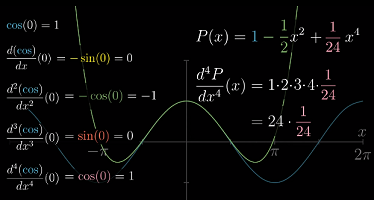
- 在非 0 点，有类似的结果，如 x=π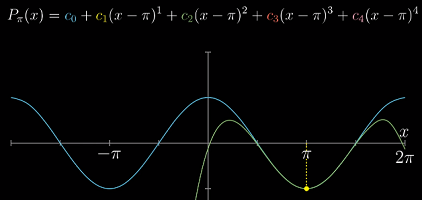
  
  带入 x=π 就能消去所有无关项
“泰勒多项式”小结
- 在对高阶多项式求导时，自然而然的出现了阶乘的形式
- 当然，真正的系数需要除以这个阶乘
- 在向近似多项式中添加更高次的项时，不会影响低次项
- 因此，多项式任意 n 阶的导数在 x=0 时的值都由唯一的系数控制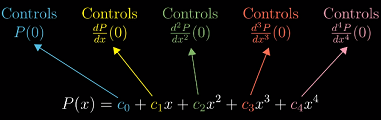
- 这样的多项式就称为“泰勒多项式”

泰勒多项式的本质

泰勒多项式实际上是利用函数在某点处的高阶导数，来近似该点附近的函数值

宏观来讲：泰勒级数把某一点处高阶导数的信息转化成了在那一点附近的函数值信息

x=0 时，它的常数项能让它与 f(0) 的值相等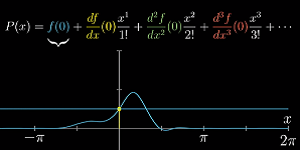
它的一次项让两者的斜率相等
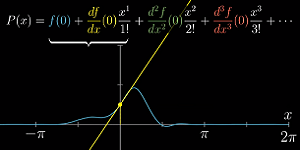
二次项让两者斜率的变化率相同
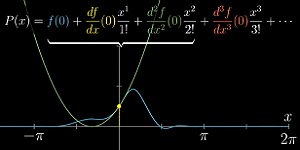
以此类推，项数越多，近似就越精确

从几何角度看二阶泰勒多项式

考虑如何近似曲线下的面积函数 f_area(x)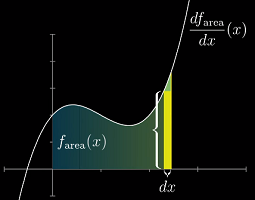
- 当 dx → 0 时，我们可以将增长的部分近似为矩形
- 但如果想将面积的变化近似得更准确，就需要考虑那块近似三角形的部分
假设已知面积函数 f 在 a 点的导数信息，想要近似在 x 时的面积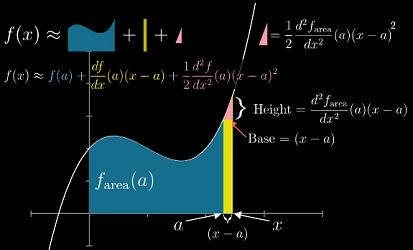

三角形的高 = 斜率 * 底，斜率 = 曲线在 a 点的导数 = f''(a)

任意函数的泰勒多项式

函数f(x)在x=0处的泰勒多项式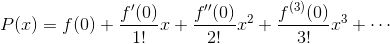
函数f(x)在x=a处的泰勒多项式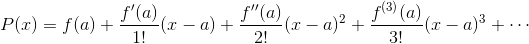

级数的概念

级数（series）的定义——无限项的和

当泰勒多项式无限累加下去，就成了泰勒级数

级数的一些重要概念

级数的收敛（Converges）与发散（diverges）、收敛半径

无限累加下去的和就“等于”级数收敛到的值；这里 x=1
- 一些级数无论你带入什么值，它的级数都会收敛，比如 e^x 在 x=0 处的泰勒级数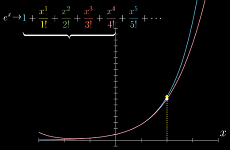
  
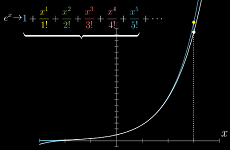
  无论 x 取何值，e^x 都等于该泰勒级数
- 但有些级数就只会在一定取值范围内才会收敛，比如 ln(x) 在 x=1 处的泰勒级数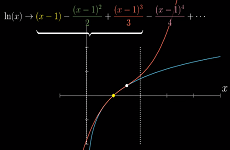
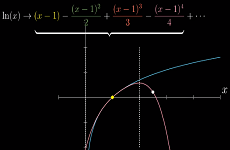
  - 只有当 x∈(0,2]时，该级数才会收敛
  - 换言之，在 x=1 处取得的导数信息无法拓展到更广的取值范围
  - 这个泰勒级数的收敛半径为 1，即x∈(0, 2]

常见的泰勒级数

泰勒级数_百度百科 https://baike.baidu.com/item/泰勒级数/7289427?fr=aladdin#6

The link of this page is https://blog.nooa.tech/articles/93227351/ . Welcome to reproduce it!