Loss Functions

背景

在优化算法中，用于评估候选解决方案的函数（即一组权重）称为目标函数（Objective Function）。我们可能会寻求最大化或最小化目标函数，这意味着我们正在搜索分别具有最高或最低得分的候选解决方案。通常，使用神经网络，我们试图将误差最小化。这样，目标函数通常被称为成本函数（Cost Function）或损失函数（Loss Function），而由损失函数计算出的值简称为“损失（Loss）”。

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。

一般损失函数

0-1损失函数(zero-one loss)

形式

0-1损失函数的计算是预测值和目标值不相等为1， 否则为0，数学形式为：

当然，这个条件有点太严苛，通常也可以方宽条件到|Y - f(x)| < T，即：

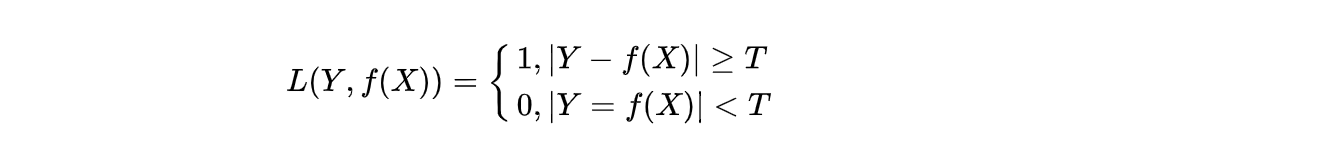
出处

• 感知机

平均绝对值损失函数（Mean Absolute Error, MAE）

形式

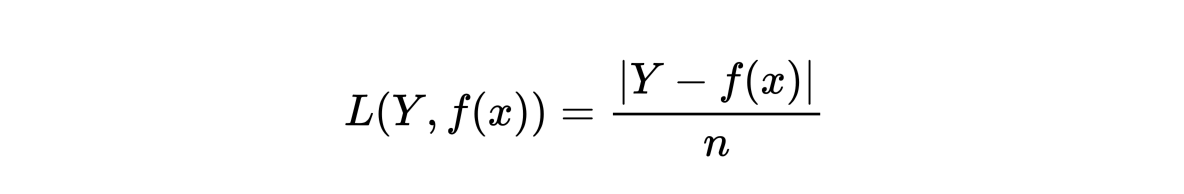
实现

def mean_absolute_error(actual, predicted):
	sum_absolute_error = 0.0
	for i in range(len(actual)):
		sum_absolute_error += abs(actual[i] - predicted[i])
	mean_absolute_error_ = 1.0 / len(actual) * sum_absolute_error
	return mean_absolute_error_

平均平方损失函数（Mean Squared Error, MSE）

形式

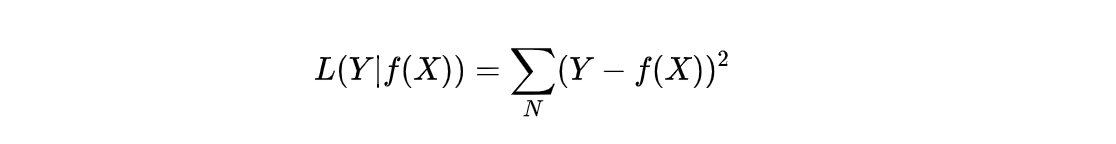
出处

• 回归问题

实现

def mean_squared_error(actual, predicted):
	sum_squared_error = 0.0
	for i in range(len(actual)):
		sum_squared_error += (actual[i] - predicted[i])**2.0
	mean_squared_error_ = 1.0 / len(actual) * sum_squared_error
	return mean_squared_error_

交叉熵损失函数（Cross-Entropy Loss or Log Loss）

形式

多个类别的交叉熵一般形式为：

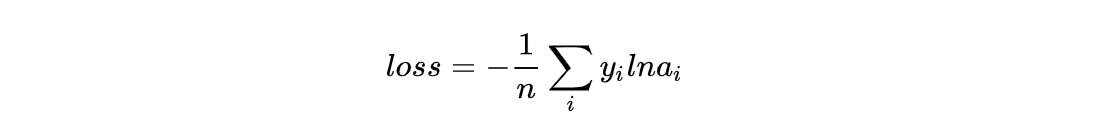
对于二分类问题，因为i只有1个值，所以也写成：

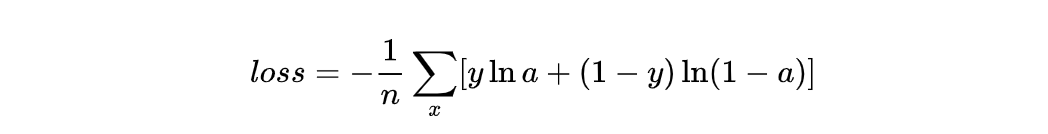
出处

• 分类问题

实现

1. 二分类交叉熵

def binary_cross_entropy(actual, predicted):
	sum_score = 0.0
	for i in range(len(actual)):
		sum_score += actual[i] * log(1e-15 + predicted[i])
	mean_sum_score = 1.0 / len(actual) * sum_score
	return -mean_sum_score

2. 多分类交叉熵

def categorical_cross_entropy(actual, predicted):
	sum_score = 0.0
	for i in range(len(actual)):
		for j in range(len(actual[i])):
			sum_score += actual[i][j] * log(1e-15 + predicted[i][j])
	mean_sum_score = 1.0 / len(actual) * sum_score
	return -mean_sum_score

合页损失函数（Hinge Loss）

形式

其标准形式为：

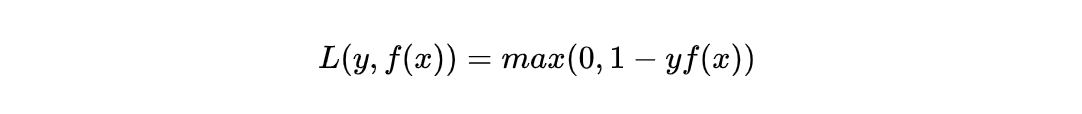
因为其在坐标系中的图形形状像书页，所以称之为合页损失。

出处

• 支持向量机（SVM）

感知机损失函数（Perceptron Loss）

形式

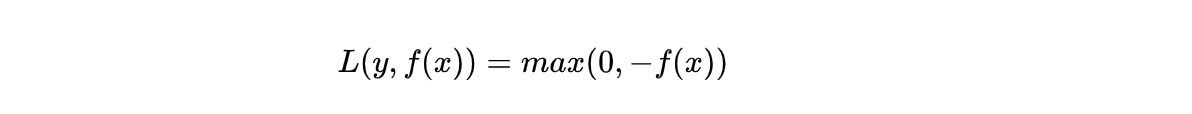
其可以看成是简化版的Hinge Loss。

出处

• 感知机（Perceptron）

The link of this page is https://blog.nooa.tech/articles/cf69cf57/ . Welcome to reproduce it!