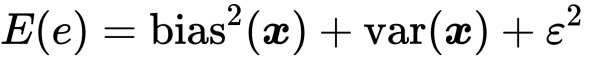误差(Error)，偏差(Bias)，方差(Variance)与噪声(Noise)

“什么是偏差、方差与噪声，以及他们是什么关系？”是机器学习中经常遇到的问题。机器学习模型的泛化性能由算法的能力、数据的充分性以及学习任务本身的难度共同决定。对于给定的学习任务，为了取得更好的泛化性能，则需要使模型预测结果与真实值之间的偏差较小（即能够充分拟合数据），并且使不同测试集输出的方差较小（即使得数据扰动所造成的影响小）。

偏差（Bias）

Bias是用所有可能的训练数据集训练出的所有模型的输出的平均值与真实模型的输出值之间的差异。
其衡量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
其计算可以由下式表示：

$$[h(x)-f(x)]$$

其中，f(x)代表真实值，而h(x)代表算法的预测结果。

方差（Variance）

Variance是不同的训练数据集训练出的模型输出值之间的差异。
其度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
其期望的计算可以用下式表示：

$$E_{P}\left[(h(\mathrm{x})-\bar{h}(\mathrm{x}))^{2}\right]$$

其中，h(x)指的是某一次训练的输出值。

偏差与方差的关系

两者的关系可以由下图表示：

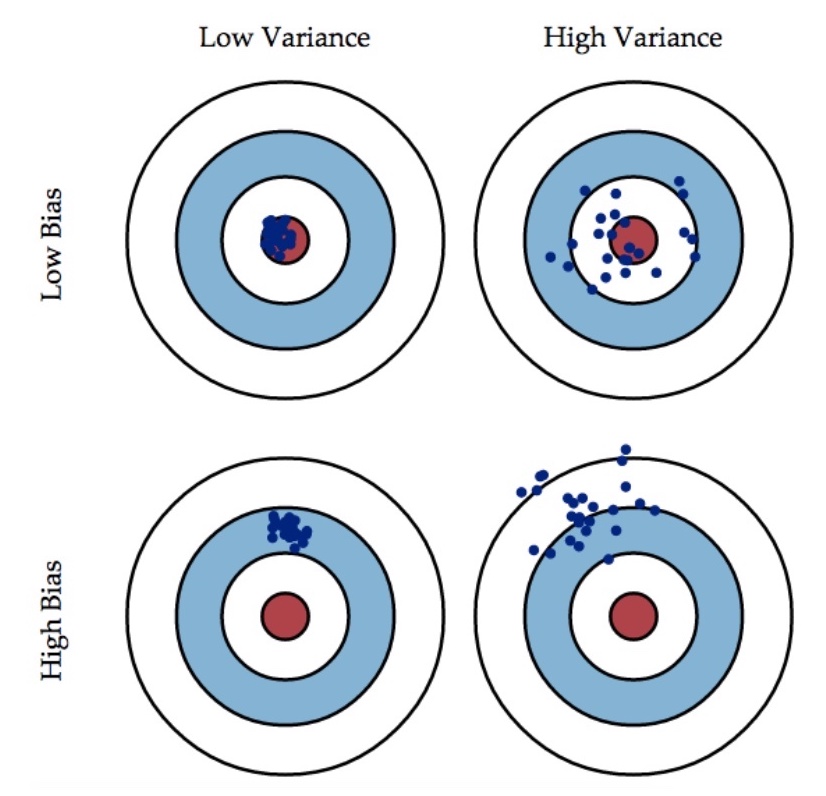
这幅图可以看出，两者可以组成四种关系，这四种关系也对应着机器学习模型的四种不同表现。

• Low Bias, Low Variance: 好模型；
• High Bias, High Variance: 差模型；
• High Bias, Low Variance: 欠拟合；
• Low Bias, High Variance: 过拟合。

于是，从偏差、方差的角度解释过拟合、欠拟合：

• 欠拟合：模型不能适配训练样本，有一个很大的偏差。
• 过拟合：模型很好的适配训练样本，但在测试集上有一个很大的方差。

减小偏差、方差的方法

1. 首先，第一个角度当然是从处理欠拟合和过拟合出发，这个角度的策略有很多，例如下面列举的几条。

   • 欠拟合：寻找更好的特征以及增大特征的维度；
   • 过拟合：增大训练集，减少数据维度，正则化，交叉验证等。

2. 另一个角度就是集成学习，而集成学习有两个主要的分支Bagging和Boosting。

   • Bagging: 这种集成的思想本身就是取多个预测结果的众数，从一定程度上是为了减小方差；
   • Boosting:这种集成思想是不断的调整学习的方向，自然是为了不断的减小偏差。

偏差-方差窘境（bias-variance dilemma）

能得到方差和偏差都很小的模型当然是最好的结果，但是事实是我们总是要取得两者的一个平衡，两者的关系可以用下图表示，这也被称为偏差-方差窘境。

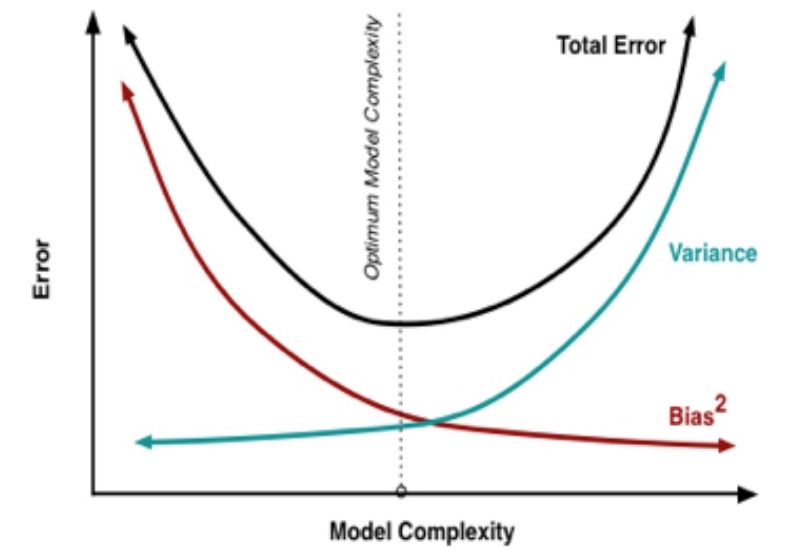
随着模型复杂度的提升，Bias会不断减小，但是Variance会不断增大，泛化误差将会呈现出先减小后增大的趋势，这个泛化误差的最小值点当然是我们的追求，所以我们在训练一个机器学习模型的时候需要平衡偏差与方差。

噪声（Noise）

噪声的数学期望可以由下式表示：

$$E_{D}\left[\left(u_{D}-y\right)^{2}\right]$$

噪声的存在是机器学习算法所无法解决的问题，数据的质量决定了学习的上限。假设在数据已经给定的情况下，此时上限已定，我们要做的就是尽可能的接近这个上限。

怎么减小噪声

因为噪声是数据本身的问题，所以减小噪声自然要从提高数据质量上做文章。一般而言，我们假设数据或者噪声都服从正态分布，其中噪声服从以0为均值的正态分布。且数据由正式值和噪声的和组成。即：

$$g_{t}=x_{t}+\varepsilon_{t}$$

1. 数据平滑法

当我们将t时刻前后n个值求平均，作为当前时刻的平滑之后的值时，得：

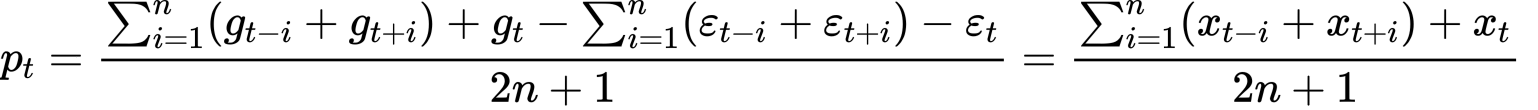
因为根据我们的假设，噪声服从0为均值的正态分布，其期望为0：

$$\sum_{i=1}^{n}\left(\varepsilon_{t-i}+\varepsilon_{t+i}\right)+\varepsilon_{t} = 0$$

2. 数据过滤法

既然数据服从正态分布，即：

$$\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)$$

那么，根据数学知识我们知道，当数据距离期望越远的时候，其越容易成为噪声点，于是我们可以将值偏离期望一定值（例如三倍标准差）的数据过滤掉。具体代码可以参考下例：

class ReduceNoise():
    def __init__(self, data):
        self.data = data
        self.len = len(data)
        self.dim = len(data[0])
    def getAvg(self, mat):
        num = [0.0] * self.dim
        for i in range(self.dim):
            for j in mat:
                num[i] += j[i]
            num[i] = num[i] / self.len
        return num
    def getVar(self, average, mat):
        ListMat = []
        for i in mat:
            ListMat.append(list(map(lambda x: x[0] - x[1], zip(average, i))))
        num = [0] * self.dim
        for j in range(self.dim):
            for i in ListMat:
                num[j] += i[j] * i[j]
            num[j] /= self.len
        return num
    def getSD(self, mat):
        return list(map(lambda x:x**0.5,mat))
    def reduce(self):
        average = self.getAvg(self.data)
        variance = self.getVar(average, self.data)
        sd = self.getSD(variance)
        section = list(map(lambda x: x[0] + 3*x[1], zip(average, sd)))
        noiseMat = []
        nonoiseMat=[]
        for i in self.data:
            for j in range(self.dim):
                if i[j] > section[j]:
                    noiseMat.append(i)
                    break
                if j == (self.dim - 1):
                    nonoiseMat.append(i)
        return noiseMat, nonoiseMat

泛化误差与三者的关系

可以证明泛化误差与偏差、方差以及噪声的数学期望的关系为：