Recurrent Neural Networks (RNNs)

循环神经网络（RNNs）

背景

RNNs在多种与序列相关的任务中都起到了很好的作用，其也是在处理时序问题的最常用的一类模型，这都归因于其计算当前时间片的时候，除了像普通DNNs使用到当前的输入信息之外，还使用到了前一个时间片的信息，其一般结构如下图所示。

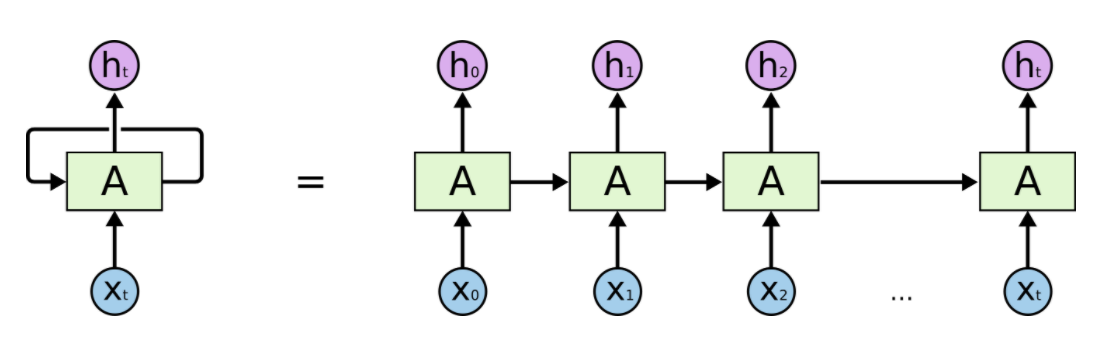
其按时间片展开的形式如下图。

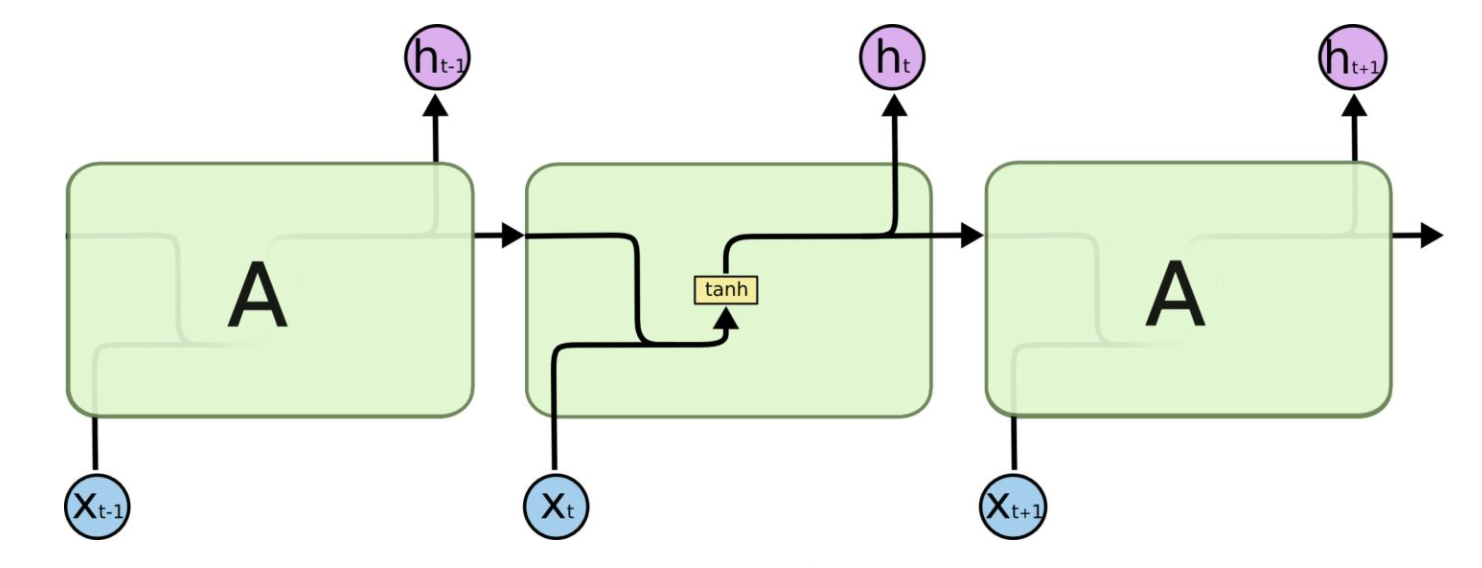
因为RNNs的考虑序列化信息的特性，使得其在许多序列化任务中发挥比较不错的效果，例如语音识别，Seq2Seq，甚至OCR（Computer Vision领域）。

形式

其数学形式可以表示为：

$$h_{t}=\sigma\left(x_{t} \times W_{x t}+h_{t-1} \times W_{h t}+b\right)$$

其时间片t - 1的输出不仅作为该时刻的预测值，同时也作为t时间片的隐状态。

(当然，也可以将传递状态和输出分开，这时预测值的形式为：$$y_{t}=\sigma(W_{t} \times h_{t})$$)

反向传播

RNN中反向传播使用的是名为Back Propagation Through Time (BPTT)方法，损失loss对参数W的梯度等于loss在各时间步对w偏导数的之和。用公式表示如下。

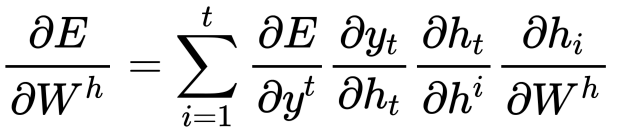
同时还有：

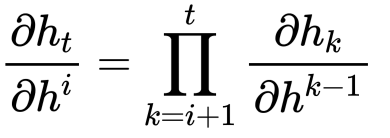
与

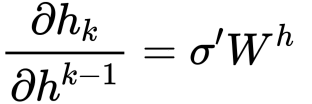
详细的反向传播过程参考 RNN BPTT。

问题

在反向传播的时候，在求时间片t到i的偏导时，结合以上两个式子，可以得到：

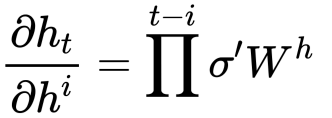
当t - i比较大时，问题来了，当$$\sigma^{\prime} W^{h} > 1$$时，连乘的结果会比较大（梯度爆炸），相反，如果$$\sigma^{\prime} W^{h} < 1$$，则会得到一个很小的值（梯度消失）。这种现象叫做RNNs的“长期依赖”。

解决方案

1. 针对“梯度爆炸”

   • 一般是采用梯度裁剪的方法。

2. 针对“梯度消失”

   • LSTM等改进的循环神经网络。

针对此问题的拓展

在深度学习发展的进程中，梯度弥散是一直存在的问题，正是因为这一问题使得深度学习模型的深度无法太深。在这个问题上也有各种不同的比较好的解决方案，例如：

• LSTM中的遗忘门
• ReLU系激活函数
• Residual Connection (Skip Connection)
• Batch Normalization

长短期记忆网络（Long Short Term Memory Network, LSTM）

LSTM提出的动机是为了解决上面提到的“长期依赖”问题。传统的RNNs节点输出仅由权值，偏置以及激活函数决定，也就是说RNNs是一个链式结构，每个时间片使用的是相同的参数。而LSTM之所以能够一定程度上解决“长期依赖”问题，是因为LSTM引入了门（gate）机制用于控制特征的流通和遗忘。其形象化的展示如下图。

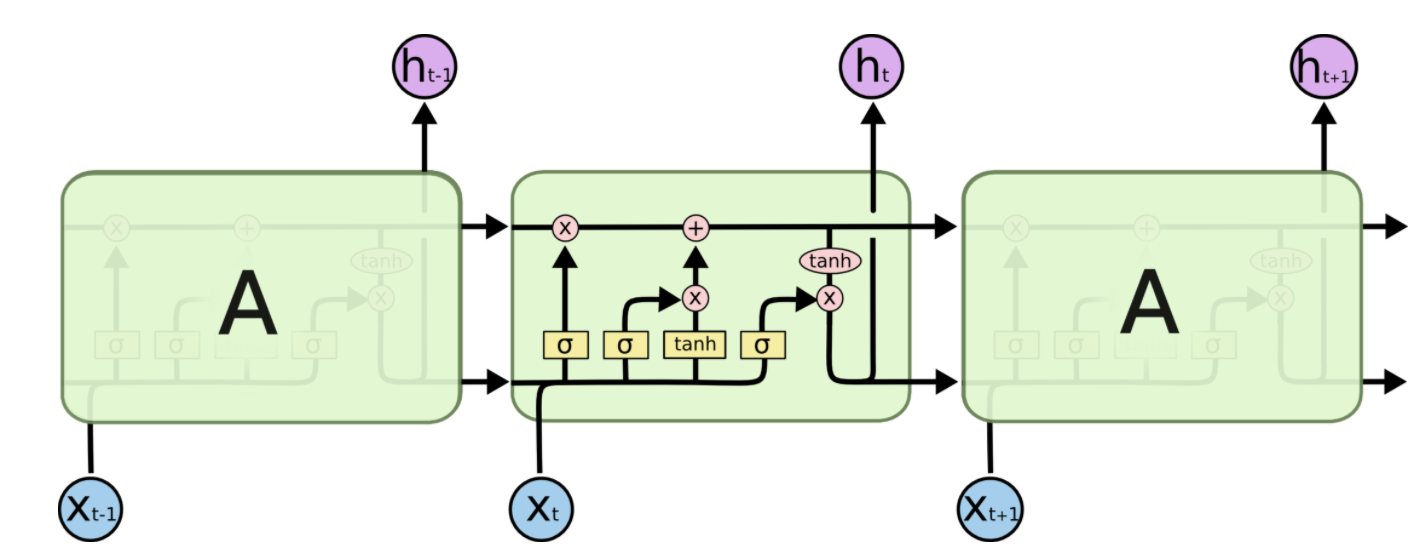
相对于RNNs，LSTM增加了一个cell state。只看LSTM一个cell state部分，如下图。

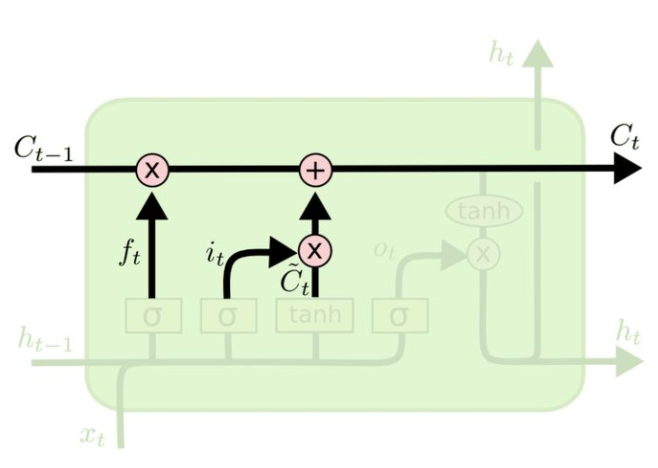
其形式可表述为：

$$C_{t}=f_{t} \times C_{t-1}+i_{t} \times \tilde{C}_{t}$$

其中$$f_t$$和$$i_t$$分别控制遗忘门和输入门参与计算的比例（他们经过了Sigmoid函数，输出结果在0 - 1之间。）

f_t$$的计算可以表示为：

f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)

在图示中的位置如下图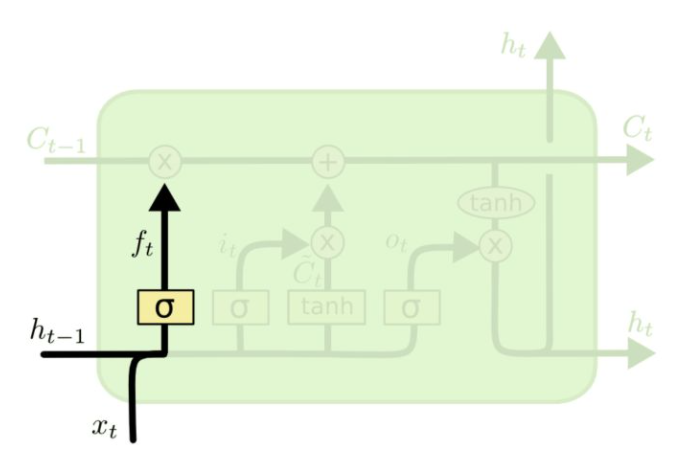：  $$i_t$$的计算可以表示为：

i_{t}=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right)

在图示中的位置如下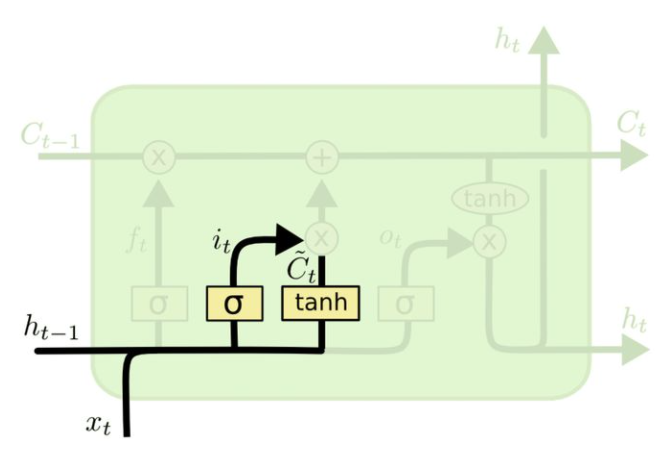：  状态更新值$$\tilde{C}_{t}$$的数学表达式以及图示如下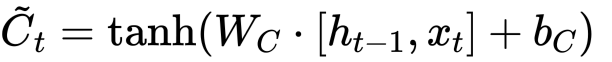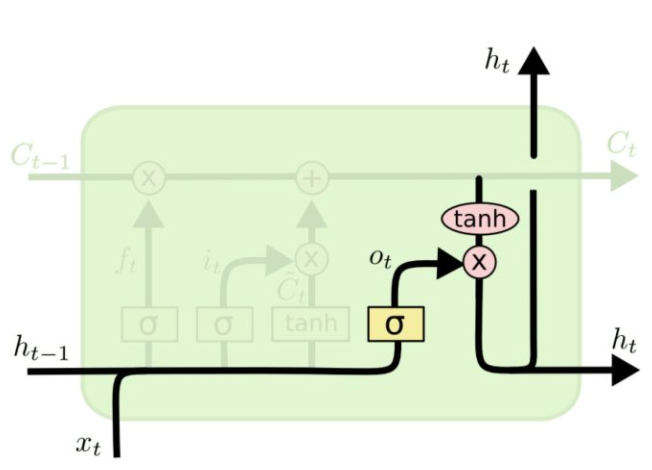：   最后，预测值$$y_t$$和生成下个时间片的输入$$h_t$$，我们需要如下计算：

o_{t}=\sigma\left(W_{o}\left[h_{t-1}, x_{t}\right]+b_{o}\right)

$$$$

h_{t}=o_{t} * \tanh \left(C_{t}\right)

## History总结 截止此处，RNNs，LSTM的发展脉络可以由下图总结。 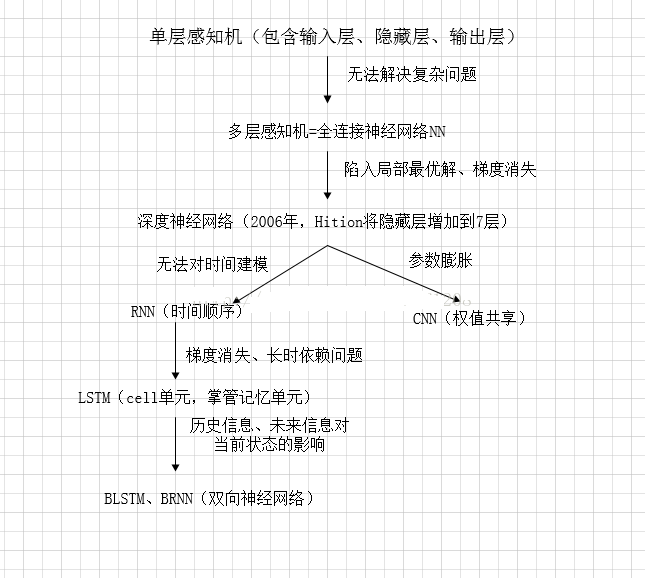 ## 参数计算 LSTM中参数的计算公式如下： `4 * [(embedding_size + hidden_size) * hidden_size + hidden_size]` # 其他RNNs的变型 ## 双向RNNs (Bi-RNNs) 有时候，为了更好地理解上下文和消除歧义，可能需要从将来的时间步中学习，于是有学者提出了双向的循环神经网络，其结构如下图所示。 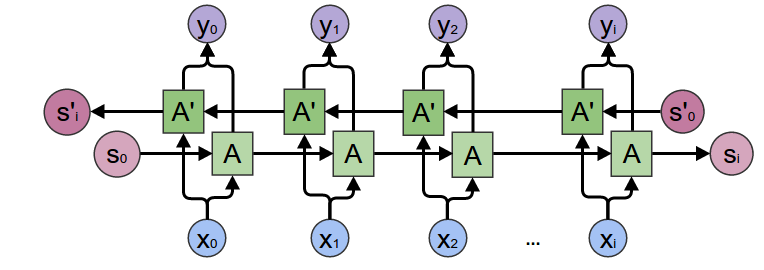 原理上讲，所有的循环神经网络及其变型都可以有双向形式。而且对于多层的RNNs，双向形式还可以有两种不同的形式，如下图所示。 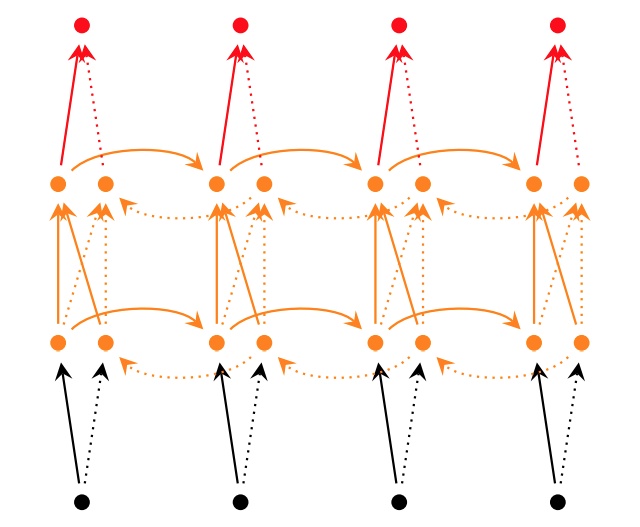 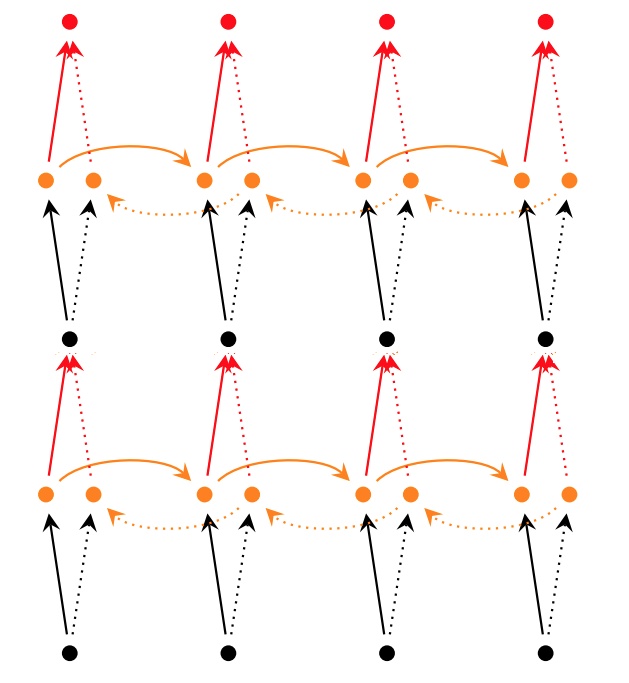 ## GRU Gated Recurrent Unit (GRU)将LSTM中的遗忘门和输入门合成了一个单一的“更新门”。同样还混合了细胞状态`C`和隐藏状态`h`，和其他一些改动。最终的模型比标准的LSTM模型要简单，也是非常流行的变体。其形式化结构和数学形式如下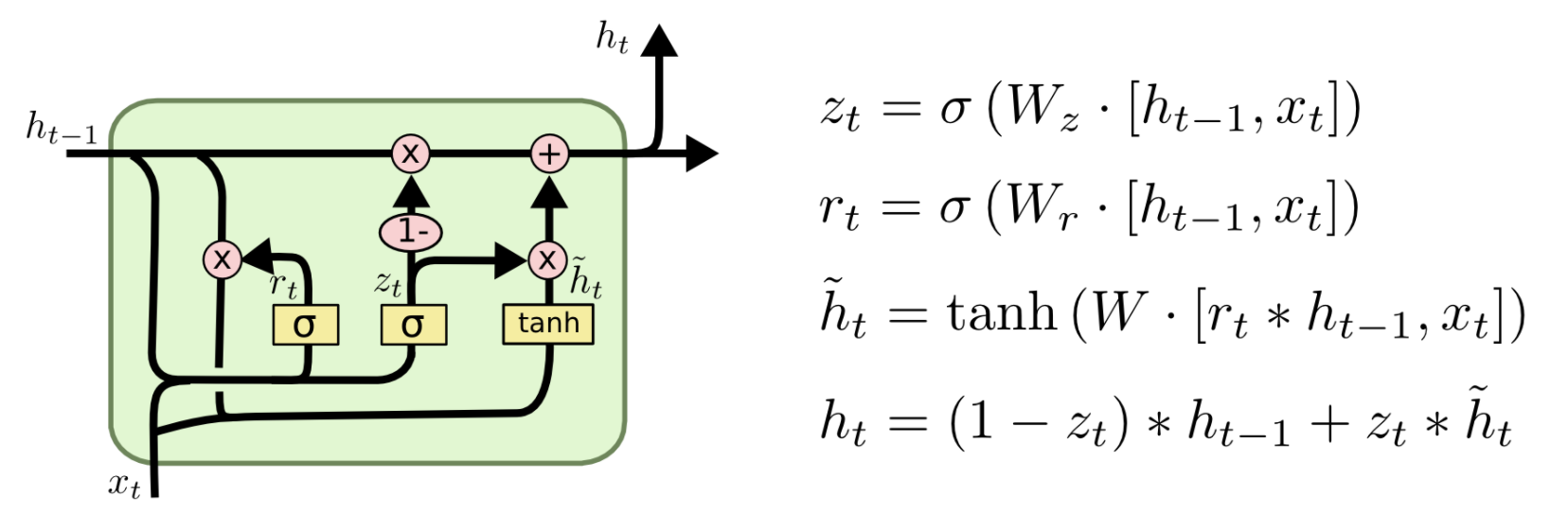：  ## Peephole Connection LSTM 其网络结构及数学形式如下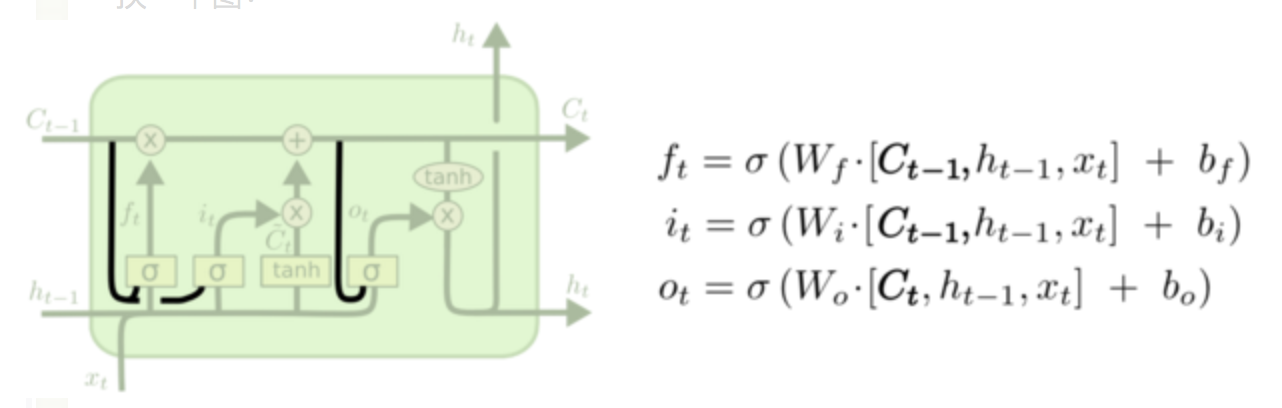：  实际上是为LSTM中的每个门的输入增加一个cell state的信号。 ## 耦合输入和遗忘门 (Coupled Input and Forget Gate, CIFG) 相比于原来的LSTM，输入门和遗忘门的因子$$i_t$$与$$f_t$$值没有太大的相互关系，在此使$$i_t + f_t = 1$$，于是其形式变为了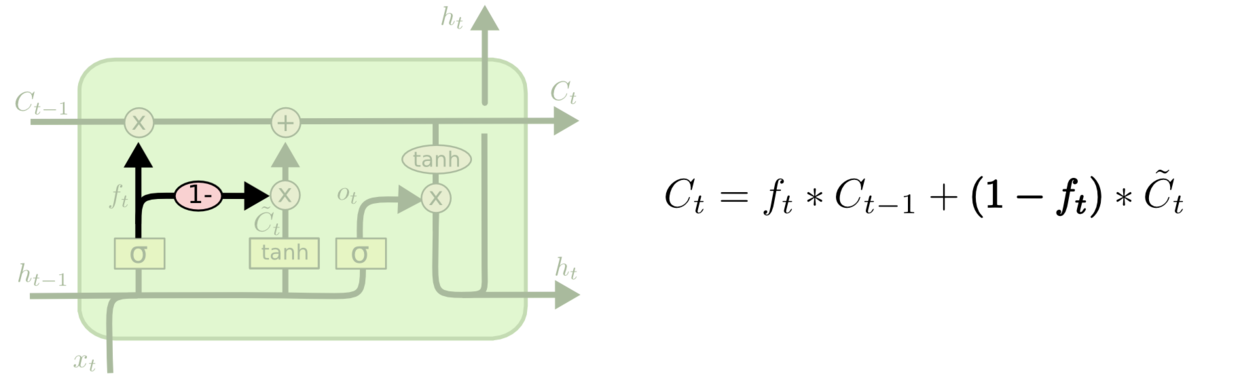：  <br><br>The link of this page is [https://blog.nooa.tech/articles/14232dff/](https://blog.nooa.tech/articles/14232dff/) . Welcome to reproduce it!